Nick Kollerstrom is historian of science, a former honorary research fellow in Science and Technology Studies at University College, London (UCL), and a former lunar gardening correspondent for the BBC. He is the author or co-author of a number of books, including Gardening and Planting by the Moon (an annual series beginning 1980), Newton’s Forgotten Lunar Theory (2000), Crop Circles (2002), and Terror on the Tube (2009)
Strong national pressure from the Egyptian government promotes the age-old concept that three Egyptian pharaohs were responsible for constructing the pyramids at Giza. Notions of ‘scientific’ rationality argue that the pyramids ‘must’ be tombs, after all they have sarcophagi in them don’t they? Thus notions of pharaonic burial as the only ‘reasonable’ explanation combine with national sentiment for claimed ownership. Against this consensus are theories that may sound airy and vague, concerning some unknown builders using methods lost forever in the mists of prehistory.
I here argue for the latter view, and suggest that two publishing events of 2007 are relevant: documentary evidence for Howard Vyse’s forgeries in the Relieving Chambers above the King’s Chamber in the Great Pyramid, published, plus a history of ancient mathematics which endorses the integrated (mathematical) ground-plan for the three Giza pyramids, by John Legon.
Non-Egyptian Maths?
While composing the ‘Geometry of the Great Pyramid’ for the Graham Hancock Forum (1), I found myself (unexpectedly) growing more and more incredulous that ancient Egyptians could have done maths like that. For a start they did not have angular measure. How could they have appreciated the amazing properties of the Great Pyramid’s unique pi/phi slope angle without that? [NB, you might wish to read the earlier math section to refresh your memory] Instead, they had gradients for measuring slope, i.e. the ‘sekhed’. I found that slopes of the descending passages were related to those of the first and second pyramids as precise angle bisections, within an arcminute – which could surely not have been done using ancient Egyptian mathematics. Bisection of a one-seventh angle is far from being a common concept, and what would it have meant to anyone confined to sekhed measure?
The Third Pyramid of Giza has a descending passage slope angle of 26° 2′ identical within a single arcminute with that of the Great Pyramid ascending passage angle – suggesting that the same construction company built both, (2) and that the exact angle within an arcminute was intentional. This was a moderately precise angle bisection, of the outer slope angle, within about four arcminutes, and lacks a straightforward Seked value (3). The 2nd pyramid’s descending passage slope angle, generally agreed to be 25° 55,’ bisects that special angle within an arcminute.
The eternal splendour of the two great pyramids at Giza involves some kind of relationship between them, and that connection is concretely expressed by two angle bisections. The First pyramid’s descending passage angle is a simple 1:2 slope, a sekhed value of two, so its angle is 26° 33′, which bisects the slope angle of the 2nd pyramid. That used the 3-4-5 Pythagoras triangle, the first in human history. We can write that exact relationship as
That is pyramid maths! That bisection surely has to be intentional. It has to be intentional because it is symmetrical, each descending passage bisecting the other’s outer slope angle. If you only had sekheds, how could you do this?
It is widely agreed that the Great Pyramid slope angle involved a use of the 22/7 pi-approximation. (4) But Egyptian maths did not ‘square the circle’ in this manner, by equating the circumference of a circle with the perimeter of a square – only the Greeks did that, aeons later. What it did (in the Rhind Papyrus, c.1700 BC) was, to find a circle having the same area as a given square, by using an 8:9 ratio. This was equivalent to having pi as 3.16, no doubt impressive for ancient times, and books compare that to the more exact 3.14 pi value expressed in the Great Pyramid’s slope angle – however, these are very different kinds of problem; only from our modern viewpoint can we move easily between the two.
The square root of two links the Great Pyramid to John Legon’s ground-plan design. (5) The distance from the top of the pyramid to the base of the King’s Chamber, in relation to pyramid height, exactly expresses the root-two value. Egyptian units of measure contain this concept, insofar as they convert from area to linear measure, (from remens to Royal cubits) but as far as anyone knows they did not have a precise value as here used.
The height of the King’s Chamber was exactly proportioned with the sole purpose (as far as anyone knows) of placing an integer 3-4-5 Pythagoras triangle in the diagonal plane of the chamber. This ingenious 3-D structure is way outside what we know about early Egyptian math. That’s enough about math arguments, which are not everyone’s cup of tea.
The Legon Ground-Plan
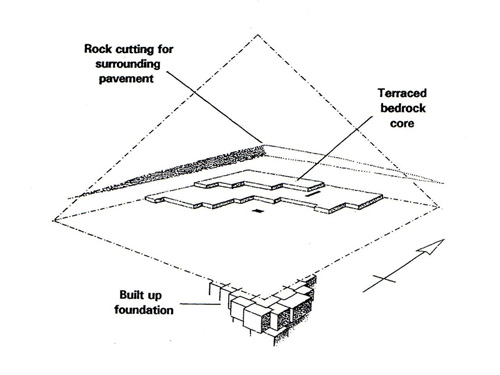
We focus here upon the Second Pyramid, as having been built upon quite sloping ground, 3-6° of incline. In one corner, a huge expanse of solid rock was ‘bulldozed’ away to make a level surface, while at the other end huge cubic blocks of three metres side-length, weighing some two hundred tons each, were used to build up the level surface. That trouble could have been avoided, by moving the site a short distance, indicating that there was something vital about that location. Quoting Robin Cook, who wrote two books about the Legon ground-plan: ‘Why else build up the eastern side of Khafre’s pyramid on a giant megalithic platform when, a short distance West, it could have been founded upon natural rock?’ (6) Ralph Ellis has also commented upon how this second pyramid had been ‘countersunk into the bedrock:’ ‘The Bronze Age solution to this defect on the topography of the chosen site was ‘simple’: just form a thick raft of megalithic blocks, each weighing in at hundreds of tonnes, and then build the pyramid on top of that.’ (7) These vast blocks were finely-jointed to fit meticulously together. (8) Ellis like others discerned a stark contrast between this ‘truly astounding’ feat and construction of other, non-Giza pyramids: ‘If one looks at the third and fifth dynasty pyramids, the engineering solutions are all simple and man-manageable.’ Imaginative accounts of toiling Egyptian slaves have failed to take account of this primary phenomenon, which shifts the whole construction back into prehistory.
Why does it do that? Around the world, stand mute records of bygone ages when vast stones could be shaped, lifted, moved and fitted exactly into position in a way that later ages would find inconceivable. At Baalbeck and Jerusalem are constructions using even larger stones, carved into a rectangular block shape. The ‘Wailing wall’ of Jerusalem is one side of a vast elevated platform on which ‘Solomon’s temple’ was long ago constructed. Three titanic carved rectangular blocks in this wall each weigh in at six hundred tons. (9) They were only properly revealed following the 1967 capture of Jerusalem. We compare these with the titanic stones at Baalbeck in Lebanon, the only place on Earth with even larger stone blocks carved and fitted into a wall, of a huge flat, raised surface; but do not speculate as to their purpose or who made them. We are merely concerned to endorse the fundamental hypothesis expounded in the books of Graham Hancock, whereby some amnesia has somehow separated our recorded history from that mythic past, maybe in the 3rd millennium BC and earlier, when cultures existed that were able to do these things.
Whatever the point was of building these pyramids, it involved the three of them being built together, if we accept the integrated ground-plan as discovered by John Legon. That involved the square root of two – and the square root of three! (10) Something was crucial about the positioning of the second pyramid. Robin Cook has expressed the view, that the Sphinx’s position can be derived from this ground-plan (11), whereas the converse doesn’t apply, the ground-plan is not derivable from the position of the sphinx.
Vyse fakes the Data
In December 1997 Graham Hancock startled everyone by being allowed a private inspection of the Vyse-discovered ‘cartouches’ in the Great Pyramid’s relieving chambers above the King’s Chamber, and announcing that they were, after all, genuine. (12) How did that affect his central thesis? On what basis did he do this, as he was not allowed to bring back any photographs with him? The sole photo of one of these daubings was shown in Lehner’s Complete Pyramids p.51 and the same a bit clearer in Sitchin’s 2007 Journeys to the Mythical past p.66 – i.e., there is only one photo! On the basis of this image it looks like a rough, 19th century imitation. (13)
Readers of this site will not need reminding, that the Vyse ‘cartouches’ are
‘The workmen’s graffiti in the ‘relieving chambers’ of the Great Pyramid had been faked by their ‘discover’ Colonel Howard Vyse, who had copied inscriptions which he had already found outside the Great Pyramid in the temples and the quarries, the presence of these inscriptions being fully consistent with the 4th dynasty ‘adoption’ scenario … What could Hancock and West possibly have seen in the relieving chambers which was so persuasive? If it was (as is claimed) certain masons’ marks which appear in the joints between the stones, then it must be emphasised that no photographs or transcripts of these masons’ marks have ever been produced (as at September 2001: there is still nothing published). In the absence of photos or transcripts it is only reasonable to presume that the marks are very indistinct …’ (14)
Mr Alford’s challenge to carbon-date the red paint used (which contains organic matter) has not been taken up: rather the contrary, one gains the impression that such sampling, like photography of the images, would be viewed with disfavor by the Egyptian authorities.
On 26th April 1837, Colonel Howard Vyse’s documentary record Operations recorded, ‘All hopes of an important discovery were not yet given up.’ He had bored a sixteen-foot hole into the Sphinx’s shoulder but found nothing much (likewise for a huge hole he made right down the middle of the 3rd Giza pyramid). Would he have to return to England empty-handed? Would his expenditure of a huge family fortune have come to nothing? Ten days later he entered the new relieving chamber which he named after Lady Arbuthnot, and lo! It was covered not only with red quarry-marks but with cartouches bearing the pharaoh’s name, Khufu. In sequence: the lowest Relieving Chamber not discovered by Vyse was bare (‘Davison’s chamber’) having no inscriptions; the next two which he blasted his way into (the ‘Wellington’ and ‘Nelson’ chambers) had red quarry-marks all over them and then finally, the chamber entered on May 7th had the pharaoh’s name.
The imaginative doodles daubed by (presumably) Vyse’s assistant J.R.Hill, on the West wall of ‘Nelson’s Chamber,’ are here reproduced. Does anyone really want to regard these as genuine Egyptian hieroglyphs? (15) People commented on how the red paint used looked ‘as fresh as if it had been painted yesterday’. (16) Gosh, fancy that.

The stonemason Humphries Brewer was employed by Vyse and in 1837 he personally witnessed Vyse employee Mr Hill entering the Great Pyramid with red paint and brush, and faking the cartouches. That is documented in the family records of Walter Allen of Pittsburgh, the great-grandson of Mr Brewer. Hill had a ‘legitimate’ purpose for entering the pyramid thus equipped, because he was painting the names ‘Wellington,’ ‘Lord Nelson’ etc on the walls of each newly-discovered chamber. Indeed we rather gain the impression it was the same red paint! (17) It is clearly documented because Mr Brewer was an honest man, and lost his job because he protested at what he saw happening, and thereby ended his contract to be in Egypt.
In the sadly-misnamed book Giza the Truth the co-authors gripe that they have not been shown documentary evidence for this important allegation (p106). Such a family record, composed in 1954 was then reproduced in the 2007 Sitchin book (p.31). This also describes how the author of this family document Walter Allen went on the local radio station to describe this record, from when his family lived in England. The 1956 record quotes Brewer’s letter home as saying: ‘… had dispute with Raven and Hill about painted marks in the pyramid. Faint marks were repainted, some were new…’ One could not expect anything much clearer. Let us hope that care will be taken to preserve this family record.
Howard Vyse’s team then went onto ‘discover’ some old bones in the 3rd pyramid and a coffin labeled ‘Menkaure’ – in a room adjacent to that containing the empty sarcophagus, in that same year, 1837. These ‘discoveries’ brought him fame and celebrity. Only many years later did carbon-14 dating show that these bones were of more recent origin by millennia, and that the ‘Menkaure’ so discovered was another pharaoh far more recent, around 660 BC; which caused this ‘discovery’ to fade out from the textbooks – although the convenient allegation that this was built by Menkaure has persisted. (18) But, we do have evidence here of an intent to deceive, do we not? The authors of Giza the Truth may not have adequately addressed this Vyse ploy of discovering a mummy and old bones in the 3rd pyramid sarcophagus (pp.61, 105; Vyse, Operations Vol. II, 85-6).
The co-authors of Giza the Truth extol Vyse as being a man of decent character. He lost the sarcophagus of the 3rd pyramid, which sunk to the bottom of the Mediterranean. His Operations describe his excitement at using his gunpowder, when bits from the back of the Sphinx’s head got blown off. (19) Others later found these bits lying around. If you wonder what kind of person would deliberately blast-damage the Sphinx, here is your answer! What kind of person would use gunpowder to get up into the ‘relieving chambers’ and use red paint to inscribe names of British military generals inside them? One should never underestimate what a man will do for the sake of immortal fame. We recommend one chapter of Sitchin’s 1980 opus, Stairway to Heaven: ‘Forging the Pharaoh’s Name,’ (20) perhaps in conjunction with the earlier account of Vyse’s work in Peter Tomkins’ Secrets of the great Pyramid.
The only statue of Khufu (‘Cheops’) is located in the Cairo Museum, in an obscure glass cabinet. It is less than three inches tall! The notion that so insignificant a pharaoh was responsible for six million tons of high-precision cut stone being assembled to geometric perfection has to be a joke – a tragic one, because it expresses the amnesia which humanity has, over its past origins. There is an inherent madness, which cannot fail to damage the logical functioning of any mind which attempts to believe it, in the idea that these edifices were constructed out of mere egoism as titanic mausoleums – and then, had no names inscribed upon them! There is nothing ‘rational’ in accepting such a view, rather the contrary. Looking at the crumbly ruins of those pyramids which his predecessors had built, in emulation of those at Giza, the question which Khufu surely asked himself was, ‘Why bother?’ Instead, he put inscriptions bearing his name nearby to the anonymous Great Pyramid, and maybe also its causeway as Alford argues. (21) His successor the pharaoh Djedefre then built a small, crumbly pyramid, which sloped at the lower and safer angle of 48°, far to the North of Giza. (22)
A scientific approach should not seek to base itself upon that which seems to be inherently nonexistent, viz corpses entombed in the Giza pyramids. Rather, it should focus more on that which does exist, namely the deep mathematical structures. The primary phenomenon here, is that the three sarcophagi were empty – like some Resurrection mystery. Equally mysterious are the three huge portcullis gates of granite slabs made to be raised and lowered independently, right in front of the King’s Chamber: surely, no reasonable person would want to claim, that these were built at the entrance to a room that served merely as a tomb?
Sequence of Construction
If indeed the ‘third pyramid’ was the first of these to be constructed – being more rudimentary in its construction then the other two and of only one-tenth their volume (23) – then we’d expect its proportions to be simpler. Its lower levels, cased in dark red granite, marked an exact quarter of its height (Petrie, p.113). Its slope angle had a 5:4 gradient. The length of its sarcophagus-containing chamber was exactly one-tenth of its overall height (24). These are simple, chunky ratios, with nothing sublime or ineffable about them – which surely, is how things begin.
The second pyramid once enjoyed that same limestone-granite division, with its two base layers covered in dark red granite, only one of which now remains (25), its only chamber being in that bottom layer. The length of the sarcophagus-containing chamber again forms one-tenth of the total pyramid height – but, this time the height measurement only goes down to that granite layer (26). Such a measure could be due to the sloping ground on which this pyramid was located.
The Second pyramid contains only blocks, it has no inner architecture: ‘What happened to the inspiration which we saw earlier in the Great Pyramid?’ mused Alford . (27) The simple answer here is, that the latter was not yet built! The Second Pyramid was a full-scale blueprint to explore how stresses and strains would manifest under Earth’s gravity. Its single, centrally-placed chamber right at the bottom would have registered these. (28)
The 3-4-5 Pythagoras triangle turns up for the first time ever, in the slope of the 2nd pyramid, then inside the King’s Chamber in the diagonal plane. Reason surely tells us, that the solid gradient was first, then the charmingly abstract concept, of a right-angled triangle in a diagonal plane came later. Thus the Great Pyramid has to be, the last. The presently accepted sequence is that in which they were ‘bagged’ by successive pharaohs.
The Great Pyramid had a 1:14 ratio between the King’s chamber length and total height (29) reflecting the 22/7 pi-ratio that it encodes. We sense deep themes of metamorphosis, connecting inner and outer, as horizontal distances across space, width of a chamber, form integer ratios to vertical height. These interconnected ratios, each maybe to 99.9% accuracy, tend to endorse the basic Legon thesis, whereby one Construction Company built all three pyramids.
An integral enterprise is here suggested, linking the three pyramids – a picture which may not be very compatible with the Hancock and Bauval thesis (1996) of an eight-millenium gap between the marking-out of an overall ‘megalithic’ framework at Giza, plus construction of the base of the 2nd pyramid, in the 11th millennium BC, and then construction of the Great Pyramid by Khufu. That is an awful long time to wait. Why would they not have completed the enterprise in that earlier time, if they had the blueprint and capability? If that base of the 2nd pyramid had been constructed millennia earlier, would builders eons later have chosen to carve out a chamber and passage deep within its base? Hancock became convinced that ‘absolutely genuine, Old Kingdom graffiti’ had been discovered by Vyse in the three ‘relieving chambers’ above the King’s chamber (30), implying that Khufu had built it. If this is the case, why have we had no modern pictures of these crucial scribbles, no team of experts surveying them, no carbon dating? Without these, the absence of quarry marks in the lowest ‘Davidson’ relieving chamber, not discovered by Vyse, remains a strong counter-argument.
The Druids of ancient Britain lacked a memory of who built Stonehenge, as Peruvian history has no memory of who made Machu Pichu, and likewise the Egyptian Government should not object to theories that date the Giza pyramids prior to dynastic Egypt – as indeed the carbon-14 tests have generally indicated. The ancient Egyptians surely derived their notion of ‘sekheds’ from these prior-existing pyramids: that of 4/5 for the ‘3rd’ pyramid, of ¾ for the 2nd pyramid, then of 11/14 for the Great Pyramid. (31)
Recording his final position, Graham Hancock wrote: ‘The Great Pyramid’s famous star shafts unequivocally link the monument to the epoch of 2500 [BC],’ (32) alluding to Robert Bauval’s conjectural ‘star shaft’ theory. The shafts in this edifice are bent and kinked, and generally blocked at one end or both: arguments over dating from alleged stellar alignments are at most suggestive. Whereas, Graham Hancock has consistently argued for a cluster of buildings at Giza ‘not erected by any historical pharaoh but dating back to prehistoric times.’ (33)
People complain there is a lack of evidence for an earlier culture that could have build the Giza pyramids. (34) Permit me to suggest that Graham Hancock’s argument about the Piri Reis map remains relevant: that this world-map derives from an original which dates back to a time before Antarctica was covered in ice, i.e. at the latest c.4000 BC; and that the team of Charles Hapgood were able to analyse this map to ascertain the location on earth from where it was projected; which they found to be Aswan, in upper Egypt. (35) Quite a lot of discerning authors have viewed the Great Pyramid as somehow representing the Northern Hemisphere (scaled by the third power of sixty, to its circumference and polar radius (36)) and this could well be relevant to whoever was able to construct that world map, millennia ago, from a site not very far away.
Were the limestone blocks used at Giza made and not quarried? New research on their material texture suggests this. Pyramid casing stones have been found to be light in density and to contain numerous trapped air bubbles, unlike the quarry samples which are uniformly dense. Microscopic examination indicates that some of the silicon-containing granules were either ‘amorphous or nanocrystalline, which is consistent with a relatively rapid precipitation reaction. The sophistication and endurance of this ancient concrete technology is simply astounding.’ (37) But, did the Egyptians have such technology? If the stones were made and not mined, this eliminates much historical conjecture – most of it, in fact. It could be time for a fresh start.
References
- 1. My article www.grahamhancock.com/forum/KollerstromN2.php
- 2. Petrie cites the mean ascending passage angle as 26°,2’30”: Flinders Petrie, Pyramids and Temples of Gizeh, 1883,2003, www.ronaldbirdsall.com/gizeh/petrie/index.htm p.61; for a different view whereby only 3rd pyramid was Egyptian, see Alan Alford, The Phoenix Solution, 1998, p.86.
- 3. John Legon does not accept this argument, viewing the Ascending passage slope as a 75:33 sekhed value, www.legon.demon.co.uk/greatpyr.htm which seems unlikely.
- 4. For a contrary view see: http://doernenburg.alien.de/alternativ/pyramide/pyr12_e.php
- 5. Legon’s ground-plan www.legon.demon.co.uk/gizaplan.htm His ground-plan used the same Royal Cubit as had Flinders Petrie in 1883, of 20.620” or 0.52375 metres.
- 6. Robin Cook, The Horizon of Khufu 1997, p.30; his diagram is here used. Cook accepted Bauval’s Orion-belt model of the three pyramids (but, Legon did not: www.legon.demon.co.uk/orion.htm), weaving the two stories together.
- 7. Ralph Ellis, Thoth, Architect of the Universe, 1997, p.21-2.
- 8. Cook, ref (6), pp.142,179.
- 9. Zecharia Sitchin, The Earth Chronicles Expeditions, 2007 Ch. 14.
- 10. Legon’s ground-plan features in How Mathematics Happened by Prof Peter Rudman, 2007 NY, p183. For a brief comment by Robert Bauval and Adrian Gilbert of the Legon/Cook geometries, see The Orion Mystery 1994, pp.53-55.
- 11. So too has Alford, ref.(2), pp.59-61, whereby the 2nd pyramid had to be present before the Sphinx was built.
- 12. See www.grahamhancock.com/features/trenches-p4.htm (or: Ian Lawton & Chris Ogilvie-Herald, Giza the Truth 2000, p.109-10.). Fingerprints, 2nd edition 2001, Intro pp.xxxiv-xxxvii; Appendix (transcript of a 1999 Horizon TV program) p.627: ‘I absolutely do accept that the Great Pyramid was built by Khufu.’
- 13. See one of the roughly-daubed cartouches at www.rickrichards.com/Egypt.htm. For the suspicious nature of inscriptions in the ‘Arbuthnot’ chamber, see Alford ref (2), p.124.
- 14. Alan Alford, http://www.eridu.co.uk/Author/egypt/giza.html (but Hancock was alone in that upper chamber, West wasn’t there). N.B., original builders’ lines horizontal and vertical exist in these ‘relieving chambers’, as Petrie wrote: ‘Some of the lines in this chamber, drawn in red on the South wall blocks of granite, are over some of the plastering, but under other parts of the plaster. These lines, therefore, were drawn during the building, and while the plaster was being laid down. A vertical line on a granite block was ‘apparently to show the builders where to place it,’ and another stone was marked by a ‘3 cubits’ line. (p.92)
- 15. Howard Vyse, Operations carried out at the Pyramids of Gizeh in 1837, Vol. 1, 1840, opp. p.284.
- 16. Comment by John Perring, one of Vyse’s team: Alford, Phoenix Solution, p.120; Sitchin, The Stairway to Heaven, 1980 p.276.
- 17. Sitchin, Journeys to the Mythical Past, 2007, 28-31.
- 18. Sitchin, Journeys, p.21; Stairway, p.277.
- 19. Mark Lehner, The Complete Pyramids, 1997, p.60
- 20. For an update on this argument, see Alford, Phoenix Solution, pp.113-125. For the central issue, see www.rickrichards.com/Egypt.htm. For a mistaken view IMO, see http://doernenburg.alien.de/alternativ/pyramide/pyr03_e.php.
- 21. Alford ref. 2, p.60.
- 22. Sitchin ref. (14), p.8.
- 23 Petrie, ref (2): ‘The whole of the pyramid, inside and outside, is so far less accurate than the two larger…’ p. 204; ‘granite just covered one quarter of the height of the pyramid,’ p.113.
- 24 Petrie ref (2) p.119, para 87; base length, p.111 para 80.
- 25 Petrie p.96, discussed in Ralph Ellis, K2, 2001, Appendix, p.105.
- 26. Petrie, p.98: chamber length 27 RCs, Ralph Ellis estimated 270 RCs for height (limestone), plus 4 RCs for its granite-base height: K2, p.135.
- 27. Alford, p71.
- 28. See Petrie’s diagram comparing these two pyramids: www.ronaldbirdsall.com/gizeh/petrie/photo/plate7.html
- 29. Petrie, pp.43, 80: 5776.0” height and 412.4” chamber length.
- 30 Fingerprints, 2001 2nd Edition, Appendix with TV interview of 1999 text, p.627.
- 31. A ‘sekhed’ ratio is the reciprocal of a tangent.
- 32. Hancock, ref. (12).
- 33 Hancock, Fingerprints 1995, p.430.
- 34. For a different view, see Michael Baigent, Ancient Traces, 1998, pp.174-8.
- 35. Fingerprints, p.463.
- 36. Earth’s polar radius scaled in proportion to GP height, to 99.8% (Fingerprints, p.460): base 60 maths was Sumerian-Babylonian, not Egyptian.
-
37. ‘Microstructural Evidence of Reconstituted Limestone Blocks in the Great Pyramids of Egypt’ Jnl of the American Ceramic Society, 2006, 89:
www.geopolymer.org/news/cutting-edge-analysis-proves-davidovits%e2%80%99-pyramid-theory
www.geopolymer.org/archaeology/pyramids/pyramids-2-the-evidences







