The world: it all runs like clockwork, doesn't it? But where did the clock come from and who decided on and defined the measures of time? The ancient Egyptians memorialized time in the Great Pyramid, by constructing it to very specific mathematical and geometric measurements, both internally and externally, and by their choice of location for it. It was the builders' ancestors who devised the measures of time and constructed the clocks with which to mark its passage. Their ancestors could track the seconds, minutes, and hours of the day. They knew the length of what we call the tropical year, which we use for our calendar, to within a matter of seconds. And, astoundingly, they knew the measure of what we call the Platonic Year or Great Year, which measures the amount of time that it takes for the equinoxes to precess through one complete cycle around the band of the ecliptic or zodiac: approximately 25,920 years. The proof lies in the Great Pyramid.
Wells-of-the-Sun
Many measures of time begin with the Sun and the ancient Egyptians were certainly very well versed in using its movements for this purpose. To observe and record the Sun's movements, the ancient Egyptians carved deep perpendicular shafts, rectangular in shape, in the ground in various locations throughout the land. Examples of these shafts can still be found, one at Saqqara under the Step Pyramid of Zoser, which was probably in use long before he built his pyramid over it, and one at the Zawyet el-Aryan Pyramid. All were most probably referred to as Wells-of-the-Sun. Exactly when these devices were placed in service and how many were constructed, will probably be lost to history forever. Given the emphasis that the Egyptians placed on the measurement of time, though, there must have been a number of them in regular and systematic use throughout the land for many, many years.
In operation they were fairly simple devices. As the Sun rises or sets in the sky, it would have reached ever deeper into or gradually retreated from the depths of these shafts. As it did so, the priests observing the phenomenon would record its maximum descent on each particular day. At the instant that this happens, the Sun reaches its maximum angular altitude above the horizon, along the meridian or longitude of the observer's location. The maximum depth of the Sun's reach down the shaft corresponds directly to its angular altitude above the horizon. This event is the meridian passage of the Sun and is known as Local Apparent Noon (LAN). Of note is the fact that the measure of the Sun's observed angular altitude at LAN corresponds directly with the observer's geographic latitude. Roughly speaking, the observer's latitude at LAN is the result of: (90°) – (observed altitude of the Sun) + (latitude of the Sun's apparent position at LAN). For example: if an observer is facing south and the Sun's altitude at LAN is observed at 50° on the day that the latitude of the Sun's apparent location is 20° North, then the latitude of the observer's position would be: (90°) – (50°) + (20° North) = 60° North. (Several correction factors are often applied to fine tune this calculation, but they are fairly inconsequential for our purposes.)
Measuring the Year of the Seasons
For all practical purposes, the Great Pyramid is located on the 30th parallel of latitude in the northern hemisphere. If the LAN were to be observed from the Pyramid's location on the day of the vernal equinox, when the Sun stands directly above the Earth's equator, its angular altitude at LAN would be 60° (90° – 60° + 0 = 30°N). It would also be 60° if LAN were observed at the Pyramid's corresponding latitude in the southern hemisphere, 30°S (90° – 60° + 0 = 30°S). Observing and recording the time of LAN on the day of the vernal equinox is of critical importance, because it is from that exact instant that the true tropical year begins. The year ends at the exact instant when LAN is observed at the next vernal equinox, when observed from the same meridian location. If we observe LAN on the day of the vernal equinox from the Great Pyramid, the sun's altitude would be 60° and it would reach that same exact altitude at LAN, exactly one tropical year later. In other words, when the Sun is observed to reach 60° altitude from the location of the Great Pyramid in the spring, the tropical year begins, and it ends when it reaches 60° altitude on the following vernal equinox. This phenomenon repeats itself every year and will continue to do so. The difference between successive LAN readings on the same meridian is exactly 365 days, 5 hours, 48 minutes, and 45.51 seconds, which is the length of the tropical or solar year.[1] LAN observation is very straightforward and measurements within a matter of seconds are easily achievable. It should be emphatically stated, though, that the location of the Great Pyramid, if LAN observations were made there at all, was only one of the many locations throughout Egypt where they were made. However, it is in its use as a symbol for this important measurement that we can appreciate the full significance of the Pyramid's relationship to it. If we sketch out an image of the instant of LAN on the vernal equinox from the Pyramid's location, this can readily be seen.
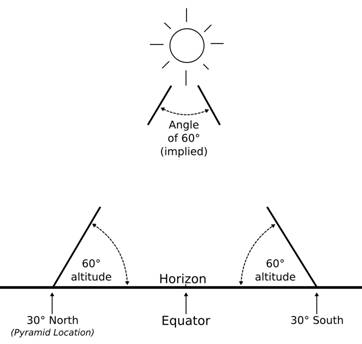
It's all a matter of geometry. The equilateral triangle (60°-60°-60°) that is formed at the vernal equinox between the Great Pyramid's location at 30° North and its corresponding location in the southern hemisphere at 30° South, with the implied angle at the Sun's apparent position above the equator, graphically defines the length of the tropical year-the year that we use for our calendar as it conforms to the seasons. The equilateral triangle is not closed at the top in the symbol because the Sun is in reality many millions of miles from this apparent location and its true angular relationship to 30°N and 30°S would be effectively zero. The importance of this symbol to the measurement of time is such that we would not be far off the mark in calling it an image of time itself, which will become ever more apparent in the following sections of this article. The equilateral triangle is used in many cultures as a symbol of heaven or perfection or unity, or all of these and more. Could its 60° angles also be the source for the number 60 that is used in the measure of seconds and minutes? It is tempting to think so. And one wonders if the true source for the Masonic symbol that appears on the back of the U.S. one dollar bill of the truncated pyramid with the shining eye above it could be this same image? (In Egypt, of course, the eye is the eye of Horus or the Sun.) The legends surrounding the symbol strongly suggest a connection with time: "He Approves our Beginning" and "New Order of the Ages." If the two images are connected, then the pyramid in the Masonic symbol holds a double meaning: it represent both the Great Pyramid as well as the equilateral triangle that forms at LAN on the vernal equinox, which is symbolic of the beginning of a new year. How profound!
Reckoning in the Heavens and Counting the Stars
The British astronomer, Richard Anthony Proctor, in his book, The Great Pyramid, Observatory Tomb and Temple, recognized that the Grand Gallery of the Great Pyramid was ideally configured and precisely aligned to observe the passage of stars in the Northern Hemisphere. As an astronomer, he had no doubt that the Grand Gallery had been used for this purpose and his argument was both detailed and compelling, and as Peter Tompkins observed in his seminal work, Secrets of the Great Pyramid, Proctor's argument has never been refuted. Proctor noted that the Grand Gallery is perfectly aligned with the Pyramid's meridian, or longitude, and that the narrow slit in the ceiling of the Gallery, which runs for its entire length at an angle of 26.3° atop high corbelled walls, permits clear observation of the stars over an arc in the heavens of some 80° along the meridian as they pass overhead. This would have enabled an observer precisely to time the meridian passage of each star as it moved across this opening from east to west. He further noted that an observer in the Gallery could also have readily measured the star's declination or angular height above the celestial horizon at the same instant that it reached its upper culmination on the meridian. Afterwards, armed with the exact measure of a star's declination and its time of meridian passage converted to hour angle measurement (hours, minutes and seconds of arc), which are respectively equivalent to earthly latitude and longitude, its precise location on the celestial sphere could be affixed with ease and plotted on a flat star chart. The stars observed could also be organized into tables according to the time of their meridian passage or hour angles and declination for ready reference and to assist with further observations.
Egyptian astronomers were no doubt well aware from long practice that the time for successive appearances of a star at an observer's meridian was shorter than the time required for the Sun to make successive LAN on the same meridian. The time between successive meridian passages by a star is 23 hours, 56 minutes, 4.09 seconds, which is known as the sidereal day[2], while the time between successive LAN meridian passages by the Sun is 24 hours of mean solar time. The difference between the two arises from the motions of the Earth in orbiting the Sun. However, timing the meridian passage of stars is more conveniently done in sidereal time than in solar time, so the Egyptians probably adapted clocks to track sidereal time in lieu of solar time for their celestial observations of the stars. The shorter sidereal day was divided into proportionately smaller hours, minutes, and seconds, than the solar day, but still followed the 24 hours/day, 60 minutes/hour, and 60 seconds/minute unit conventions of the solar day, with the sidereal second equal to 1.00274 solar seconds. Both solar time and sidereal time are arranged in hour angles along the equator, which gives rise to what are now called time zones. This enables time to be converted to longitudinal measure and vice versa. Using hour angles, one hour of solar time and one hour of sidereal time are both equal to 15° of longitude.
The solar day begins at midnight, 00 hours and 00 minutes, each day. By longstanding convention, probably going back to remotest antiquity, the sidereal day begins when the meridian or hour angle of the Sun's vernal equinox LAN crosses an observer's meridian. In this respect, the Sun's vernal equinox LAN meridian functions as if it were a star chosen to mark the beginning of a new sidereal day. Vernal equinox LAN is the starting point, 00 hours and 00 minutes, for the sidereal day and it is prominently marked on star charts and tables. A sidereal day runs from the meridian passage of the vernal equinox LAN at an observer's meridian to its next meridian passage. The vernal equinox LAN meridian is simply its location at any given moment from an observer's meridian, as measured by the local sidereal clock (e.g. if it is 22:00 local sidereal time, the vernal equinox LAN meridian is 2 hours east of the observer's meridian). The meridian passage of each and every star can then be timed from this point forward. (It is tempting to speculate that the ancient Egyptians used the Great Pyramid's meridian as the Greenwich-equivalent of the starting point for the sidereal day and the solar day as well, but exactly which location was accorded this honor back then is not known.)
After marking the vernal equinox LAN meridian on the star charts and tables, it is then easy to determine from them which stars were present in the Sun's celestial background-the band of the zodiac-and precisely where the Sun was located with respect to this background at that instant, even though the stars were not visible in the bright light of the noon Sun. All of the stars in the band of the zodiac are visible in the night sky at some point during the year and can be observed and measured. Once comprehensive star charts and tables are prepared, repeat observations and measurements are not necessary. However, all of the meridian times will have to be adjusted to the new vernal equinox LAN meridian time. It is important to remember, though, that the Sun's sidereal year runs between successive appearances at the same vernal equinox LAN meridian, and is 365 days, 6 hours, 9 minutes, and 9.54 seconds in length.[3] (Not to be confused with Earth's sidereal year, which is 366.24 sidereal days in length.)
Precession of the Equinoxes and its Measurement
First off, it needs to be categorically stated that observing the effects of precession in the star patterns that are visible in the heavens above the point of sunrise during twilight on the morning of the vernal equinox is not practical, and measuring it is out of the question. The stars are visible for quite some time during twilight and there is no fixed frame of reference with which to observe them from in order to compare their measurements from year to year. If observations were made over thousands and thousands of years, all that could be said is that the stars visible just before dawn on the vernal equinox were slowly changing. There is a far more accurate and easier method for observing and measuring precession, and it no doubt was the same one followed by the ancient Egyptians. It simply involves measuring LAN on the vernal equinox over successive years and marking the event on the star charts and tables as described above.
When the exact instant of the vernal equinox LAN is observed and timed, and then entered onto the star charts and tables, it becomes readily apparent that there is a discrepancy of some 20 minutes and 24 seconds from the time of the previous year's observation. With clocks designed to measure within fractions of a second this is very significant. And if there was some concern about human error possibly having contributed to the discrepancy, an observation of the event the following year would have removed all doubt. LAN was occurring 20 minutes and 24 seconds sooner than the sidereal clock called for and no matter how many times successive LAN observations were made, there was an almost constant difference between the Sun's sidereal year (365 days, 6 hours, 9 minutes and 9.54 seconds) and its tropical year (365 days, 5 hours, 48 minutes, and 45.51 seconds) of 20 minutes and 24 seconds. (Recall that the sidereal year is the measure of time between the vernal equinox LAN meridian, as marked on the star charts and tables, and the return of this meridian to that same position one year later. Also recall that the tropical year is the measure of time between successive occurrences of the Sun's LAN on the vernal equinox.) This is a precise measure of both the sidereal and tropical years, which leads to a precise measure of precession. By entering successive occurrences of vernal equinox LAN on the star charts and tables, it can readily be seen that the background stars are changing, as the event regresses through the 12 houses or signs of the band of the zodiac-72 years per degree, 2,160 years per sign, 4,320 years for two signs, etc., until vernal equinox LAN returns to its original starting point 25,920 years later.
If all of this sounds complicated, it's not; it's merely a detailed explanation for a procedure that is very straightforward and the very essence of simplicity. The first step requires an observer to note the exact instant when the Sun reaches a maximum altitude of 60° above the horizon at the Great Pyramid's location in the spring, and to mark both the solar and sidereal time clocks. The time on the sidereal time clock is then entered onto the star charts and tables, and corrected to 00:00. The sidereal clocks are reset to 00:00 also. Thereafter, all star observations are timed from the vernal equinox LAN meridian, 00:00, going forward. Then, when the Sun again reaches a maximum altitude of 60° from the Pyramid's location the following spring, the whole process is repeated.
The time span between the two readings on the solar clock is the length of the tropical or solar year. Meanwhile, the time showing on the sidereal clock will be 23 hours, 39 minutes, and 33 seconds, as the location for the previous vernal equinox LAN meridian is still some 20 minutes and 27 seconds east of the Great Pyramid's meridian. This difference between the time observed for the most recent vernal equinox LAN on the sidereal clock and the location of the previous vernal equinox LAN meridian, as marked on the star charts and tables, is precession-20 minutes, 27 seconds ( 20 minutes, 24 seconds of solar time). It is that simple.
So, where then is the proof in the Great Pyramid that the ancient Egyptians knew of and measured the precession of the equinoxes? It is in the Pyramid's diagonals. On a flat projection map of the Earth, with the Great Pyramid's location at 30°-00' North latitude and 31°-09' East longitude marked off, if a line is drawn perpendicular from the Pyramid's location to the equator, the measure of this line is a distance of 1,800 geographic miles (6,000'/mile; 60 miles/degree of latitude). Then, if the Pyramid's diagonals are extended from the Pyramid's location down to the equator, the measure of the distance marked off by the intersection of the diagonals with the equator is a distance of 3,600 geographic miles.
This distance, 3,600 miles, leads to several relevant facts. It is 1/6th of the circumference of the Earth, or 60° of its equatorial arc. (There's that number 60 again that is associated with the equilateral triangle!) But more importantly for our purposes, the distance marked off by the diagonals also marks 1/6th of the Great Year or 4,320 years, which is two ages of the band of the zodiac. There's the proof, and since the Pyramid's diagonals mark off this measure of 4,320 years on the equator, precisely where the Sun stands on the vernal equinox when all critical measurements of time were and still are made, it would seem to be definitive.
This number-4,320-is widely recognized as a universal sign or marker for precession and the Great Year throughout the ancient world. (For an excellent summary of the attention paid to this number by ancient cultures, see Graham Hancock's Fingerprints of the Gods, Crown Publishing; Part V, "Mystery of the Myths: 2. The Precessional Code" and Chapter 48, "Earth Measurers.") This number is evidence that the ancient Egyptians not only knew of the precession and could measure it with precision, it further demonstrates that the location of the Great Pyramid was not chosen randomly or by chance. The ancient Egyptians knew precisely where they wanted it located and it was with these measurements of time in mind, among others, that they placed the Pyramid there.
Why the seeming fascination with the number 4,320 held by many of the ancient cultures? I believe it is one of the principal factors in a system of universal datum that they devised to integrate all measures for time, distance, weight, etc. with one another. They considered the system perfect and to have derived from a divine plan or order in the universe. They also believed that if God had touched the elements of creation, then the universe would have conformed to this system and it would have been perfect. Instead, he entrusted creation to the lesser gods, and because of this it was not created perfect. In Egyptian mythological terms, it was Ptah who designed the universe, but it was Atum-Re who created it according to the plans devised by Ptah. However, all of this, though important, is a subject that might best be addressed at another time.
Footnotes:
- American Heritage Science Dictionary (online); see solar time; Houghton Mifflin; 2002 [back to text]
- Ibid., see sidereal time [back to text]
- Ibid., see sidereal time [back to text]






