This is the story of a quite extraordinary synthesis in the history of archaoastronomy, as the bare bones of an advanced astronomical system are revealed for the first time in a thousand years. It is also the story of two numbers that underpin life on Earth and shape our local reality. And finally it is the story of three non-academic scientists and their quest to tackle some of the most enigmatic questions of our times.
The Inner Planets
Here’s my own part in this breakthrough. For the last 20 years, in my spare time, I have been studying the geometry and harmony of the solar system, with particular focus on the way that the inner planets, Venus and Mercury, relate to the Earth. In 1993 I published an observation concerning the orbits and sizes of Earth and Mercury, which had struck me as somewhat eerie. Here is a picture. What I had discovered was that a pentagram produces Mercury’s mean orbit from Earth’s, and that the same proportion relates the physical sizes of the two planets, really quite accurately (see my book for exact figures). At the time I tagged this as an interesting double coincidence, which it remains. But I also observed that an octagram could perform the same function (or very nearly). So five and eight perform a similar function.
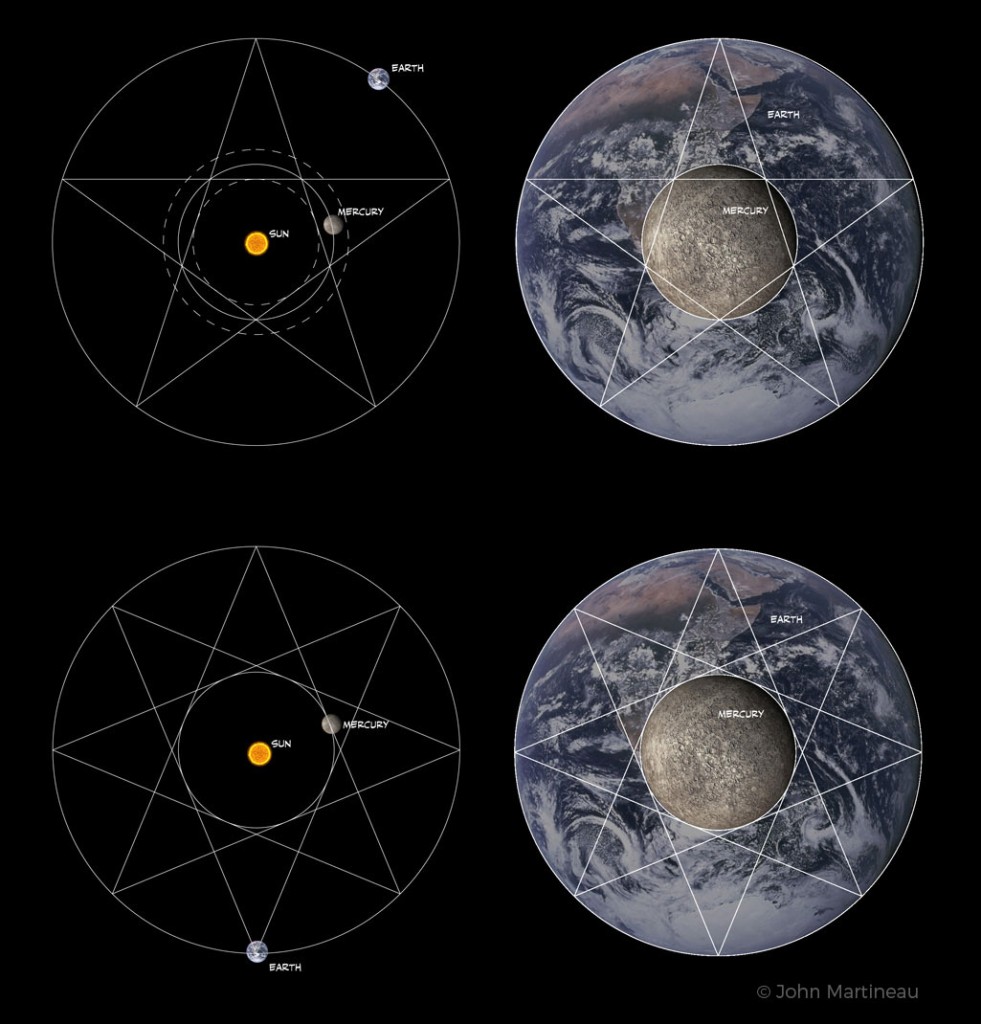
Fig. 1. Five and Eight at work in the inner solar system. A pentagram defines Mercury’s orbit from Earth’s, or the size of Mercury from the size of the Earth. And an octagram does the same thing.
A year later I was studying at the Prince of Wales’ Institute of Architecture in London under Professor Keith Critchlow. Critchlow had been supervising my astronomical musings and one morning he passed my desk and handed me a copy of a slim book, Movements and Rhythms of the Stars, by Joachim Schultz. It was a bombshell. Instead of looking at the solar system with the sun at its centre, Schultz returned the reader to their everyday experience of the heavens. He argued that whatever models we might build we actually still live on Earth, and we watch the planets from the surface of the Earth. In particular, Schultz’s book contained an accurate diagram of the way Venus moves around the Earth. Years later I wrote a computer program to plot this for myself, and recently even made a poster of it. Here it is:

Fig. 2. The beautiful Dance of Venus. Venus draws this fivefold pattern around Earth over eight years, or thirteen Venus-years.
This image shows the extraordinarily beautiful diagram of our home planet’s dance with our closest neighbour, Venus. Seen from Earth, Venus orbits the Sun every 584 days as the Sun moves around the stars every year. She comes close to Earth, between us and the Sun, five times before she goes over her trail again (almost). And what is particularly interesting here is that Venus draws this beautiful five-petalled flower in the sky around us over exactly eight years. So five and eight again.
Now five and eight are of course Fibonacci numbers, widely used by life on Earth. Most flowers have five petals. We have five fingers. As children we have five teeth in each quarter of our mouths. These fall out and are replaced with eight teeth in each quarter. Thirteen in all. And all around us on Earth, most plants and flowers and seeds and leaves, from pussy willows to pineapples use the numbers 5, 8 and 13 in spiral phyllotaxis, while in the sky above us our nearest neighbour Venus draws her five-petalled flower every 8 Earth years, or 13 Venus years.
I specialise in coincidences in the solar system, and this is one of the biggies. It’s very simple, very obvious, and very beautiful, yet it does not appear in any modern astronomy book.

Fig. 3. Life on Earth is dominated by the numbers 5 and 8, from fingers and toes to the most popular number of petals, from the numbers of our teeth (5 in each quarter as a child, followed by 8 in each quarter as an adult), to the numbers of spirals on pineapples and seedheads.
The Mayan Calendar
In my day job as a publisher and editor I get to meet a lot of interesting people, and in the winter of 2006 I found myself spending a lot of time with Geoff Stray. Tall, blond, and with a handlebar moustache, Geoff is a fascinating figure in Mayan studies. Hugely respected in the field, he has made important contributions to the understanding of the Mayan calendar, acknowledged by academics and non-academics alike. When he’s not restoring classic motorcycles, Geoff puzzles over tiny details of this vanished civilization that most people would never consider important. I had known Geoff for some time, but it was only when I started working with him on his little book for our international series that it became clear to me that I was in the presence of a walking encyclopedia.
Initally I was confused by the Mayan calendar. The core of the system dates at least to the 5th century BC, possibly much earlier, yet it seemed a mess. They even had an unadjusted 365-day cycle known as the Haab. We all know there are 365.25 days in a year. Right? Well the Maya didn’t adjust their Haab every four years.
But as I worked with Geoff on his book, drawing diagrams and typesetting tables, I began to see that the Maya were after much bigger fish. Their various calendars cleverly modelled the solar system as seen from Earth. Their various cycles, like the 260-day Tzolkin, or the 365-day Haab, were gearings to model eclipse cycles and other syntonic (Earth-centred) planetary patterns.
This was around the same time that the first working models of the famous Antikythera Mechanism were being produced. The Antikythera Mechanism is an ancient Greek metal clockwork device dated to 200BC, which models the solar system and predicts eclipses. Essentially it is a mechanised version of the classic Ptolemaic system of astronomy. Geoff and I began to wonder if the Mayan calendar, likewise, would work as a device. After coming across various papers suggesting that the late Maya might have introduced the late 819-day cycle to include Jupiter and Saturn into their calendar, we started to draw a diagram. Here it is:
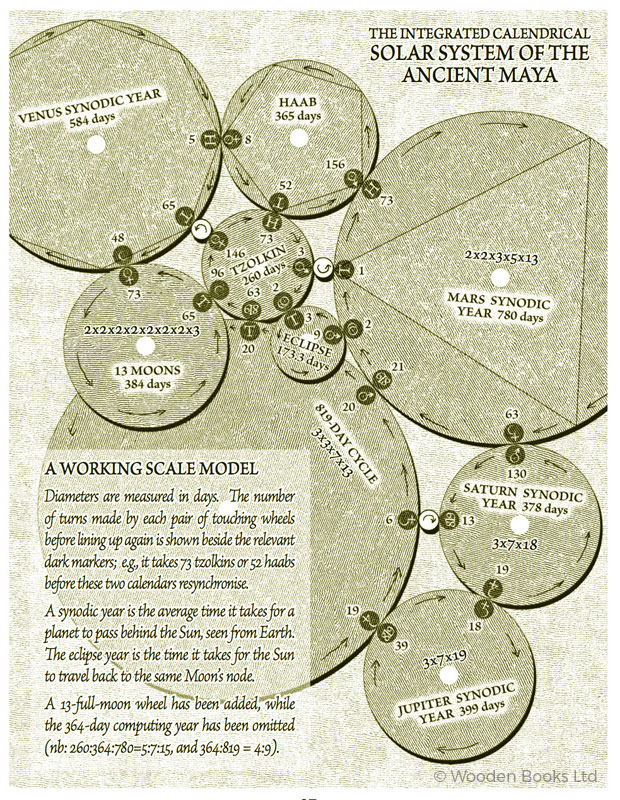
Fig. 4. The Mayan Calendar as a working model. Notice how the 365-day Haab perfectly meshes with the 584-day Venus synod in the ratio 5:8. From The Mayan and other Ancient Calendars, by Geoff Stray, Wooden Books 2007.
This is the solar system as modelled by the Mayan calendar. If you built this device out of wood, it would enable you to predict conjunctions, eclipses and more. You can see how Earth’s neighbours are neatly embodied in this synthesis. The 260-day Tzolkin is one third of Mar’s synodic year, and 3/2 times the eclipse year.
And there, at the top, the 365-day Haab relates perfectly as 5:8 with Venus’ synodic year. So the Haab is there to keep track of Venus, and emphasises the 5:8 relationship between Earth and her closest neighbour.
The Maya had one last calendar, the Long Count. This was based on a 360-day unit, the Tun, 20 of which make a Katun, 20 of which make a Baktun (144,000 days), 13 of which make a Sun (5,125 years). What was the Long Count for? In 2012 one of these 5,125-year cycles famously came to an end. But what did it mean?
In 1987 Jose Arguelles had argued that five Suns equalled a period of 25,625 years, a length of time he claimed represent the precession of the equinoxes. Precession is caused by the slow rotation of the Earth’ axis. It gives rise to a circle of pole stars, and has the effect of displacing the rising of an easterly star by 1 degree every 72 years. Arguelles’ claim was given an additional boost in a 1998 book by John Major Jenkins. In it he claimed that the 2012 end date for the current Mayan Sun was hugely significant. To understand why we quickly need to do some basic astronomy.
Each year, as the sun travels across the stars as seen from Earth, it passes through the Milky Way, the plane of our galaxy, twice. But here’s the odd bit: due to a coincidental alignment, one of these places where the Sun crosses just happens to be the centre of the galaxy, which means that once a year the Sun, as seen from Earth, lines up exactly with the galactic centre. And here’s the even odder bit: at this time on planet Earth, this happens on Midwinter’s Day. Jenkins claimed that the fact that the 2012 end date for the current Sun occurred at a time when the annual galactic solar alignment was happening at a solstice was hugely significant, and demonstrated the Maya were far more astronomically advanced than previously suspected.
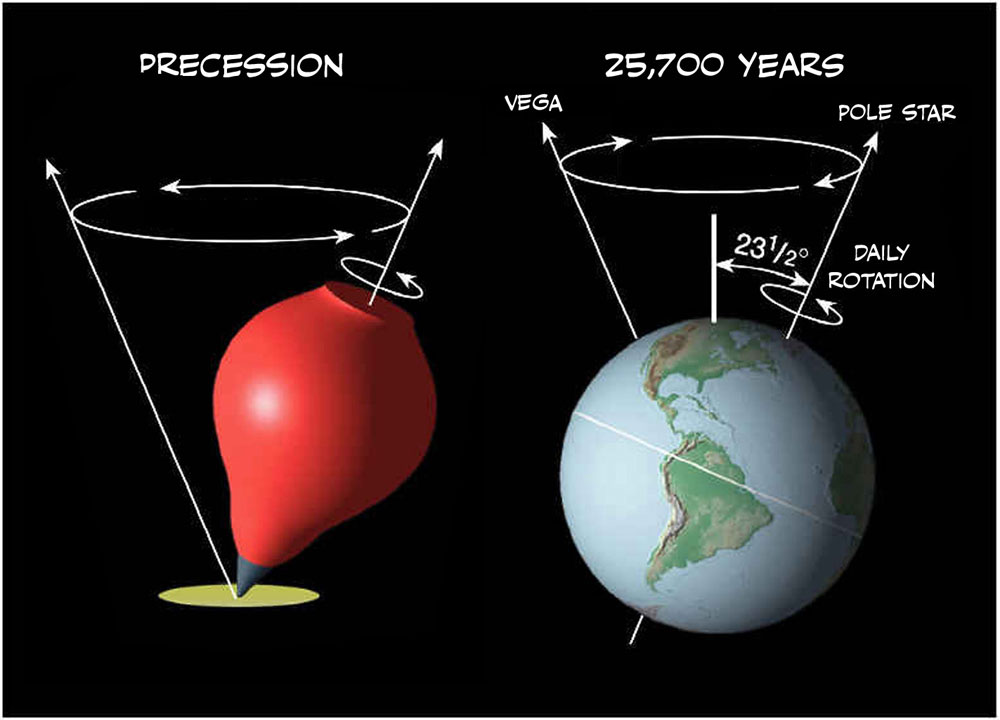
Fig. 5. The precession of the equinoxes is a 25,700-year cycle caused by a rotation of the Earth’s axis, much like a spinning top rotates as it runs down.
Fig. 6. The solar system and the galaxy. The plane of the solar system is tilted at 60.0 degrees to the plane of the galaxy. The midwinter sun is shown lined up with the centre of the galaxy, a alignment which occurs every 25,700 years and which peaked at the midsummer eclipse of 1999, and which the Mayans may have reckoned at December 2012.
We know that ancient cultures were interested in precession. The ancient Egyptians tracked it, passing down a value of 25,920 years. And it also now appears that the recently unearthed oldest buildings on the planet, at Gobleki Tepe on the Turkish/Syrian border, were built to track precession, with structures being covered up after 1,000 years and new ones being rebuilt to realign with important stars that had moved by some degrees. It’s not too far a stretch to imagine that the ancient Maya might also have tracked this long cycle and incorporated it into their Long Count.
Changing Solstices
So to the final character in this story. Once upon a time a young Englishman, the son of Salvation Army parents, fell in love, went to live in France and never came back. Thirty years later Howard Crowhurst still lives in the small village of Plouharnel in Britanny. What Howard didn’t initially realise when he landed in France was that Plouharnel was in the middle of the largest concentration of ancient standing stones in the world and that he would one day end up solving one of the strangest megalithic puzzles on Earth.
The stone rows of Carnac puzzle archaeologists deeply. Over 10,000 standing stones were erected on a vast site from 4,500 BC in multiple rows, circles, egg-shaped structures, dolmens and passage graves. Professor Alexander Thom, the renowned surveyor of megalithic sites, studied the site in the 1970s and established that its builders had been studying sun and moon alignments, sometimes tens of miles long, using the largest menhirs ever erected in Europe.
This is not the place to go into Crowhurst’s startling conclusions. Suffice it to say that that Carnac emerges as the primary university for the European megalithic sciences. One of the key things about the latitude of Carnac is that the 5-long diagonal of a north-south aligned 3-4 rectangle built here will give you the sun’s extremes (the solstices), while the diagonals of a square will give you the lunar extremes.
And it was while studying long distance solstice alignments that Crowhurst began to notice a problem. Many of the alignments still work perfectly today, but they can’t have when they were built. Why not? Because of a second long period cycle, known as the Variation of the Earth’s Obliquity. What is this?
The Earth’s axis is tilted relative to the plane of its orbit and it’s this tilt, which gives us our seasons. No tilt would give no seasons, but the tilt of the Earth oscillates from 22.1 degrees to 24.5 degrees and back again over 41,040 years. When the Earth is more highly tilted we experience more extreme seasons, hotter summers and colder winters. Right now we’re almost exactly in the middle of the cycle with an axial tilt of roughly 23.4 degrees.

Fig. 10. Over 41,000 years the tilt of the Earth oscillates between a minimum of 22.1 degrees and a maximum 24.5 degrees.
So Crowhurst began to wonder if megalithic peoples might have been interested in the 41,000-year cycle. At a practical level, bigger tilts give more extreme solstices, hotter summers and colder winters. One of the sites he examined was Maeshowe in the Orkney Islands, close to the recently unearthed extraordinary complex of sites on the Ness of Brodgar, which was buried in the same way at the sites at Gobleki Tepe.
Maeshowe is one of the best preserved megalithic chambered cairns in the world. As with other great chambered cairns of the same period, like Newgrange in Ireland, its long chamber points like a great telescope at the rising position of the midwinter sun. Crowhurst discovered that while the Sun today rises straight down the passage, at the time it was built the sun would have risen off axis, as it will do thousands of years in the future on the other side. In fact the design of the passage seems to be optimised to measure the changing position of the midwinter sun, and track the 41,000-year obliquity cycle.
A far-fetched claim, you might think …

Fig. 11. Maeshowe in the Orkney Islands, showing how the passageway aligns to the centre of the 41,000-years wing of the midwinter sun.
The Secret of the Long Count
In the summer of 2012 I visited Carnac, accompanied by Geoff Stray. Howard Crowhurst runs an annual midsummer conference there and we had been invited to speak at the 2012-themed event. Halfway through his presentation, Crowhurst was describing his hunches surrounding megalithic awareness of the 41,000-year cycle, when he casually mentioned a startling fact:
The 41,000-year cycle very precisely consisted of eight Mayan Suns.
I did a double take. Eight suns, but five made precession! Startled, I cornered Geoff Stray. He had already come across the eight Suns figure for the obliquity cycle, but not realised the significance of 5:8, while Howard Crowhurst had been unaware of the fact that five Suns gave a value for Precession. We had cracked it.
One Mayan Sun is 5,125 years.
Five Suns give the Precessional Cycle
5 x 5125 = 25,625 years (current value 25,700 years, 75 years out)
Eight Suns give the Earth’s Obliquity Cycle.
8 x 5125 = 41,000 years (current value 41,040 years, 40 years out)
Five and eight! The two long cycles that most affect the Earth relate as 5:8 and are both encoded by the Long Count. The Maya must have known. No wonder they drew so many pictures of jawbones. Five and eight! The same two numbers displayed by human teeth are the same two numbers as those used by the plants all around us, and these are the same two numbers that connect us with our closest neighbour Venus, and the same two numbers that relate the two long cycles that affect Earth-bound astronomy.
Conclusion
We live at a very special time right now. Our midwinter sun lines up like an arrow aimed at the heart of our galaxy, while our tilt is exactly midway through its wobble. These two cycles have not aligned in such a spectacular fashion since homo sapiens walked out of Africa, nor will they realign for another 100,000 years. This is the time that any astronomer/astrologer worth their salt would indicate as being a singularly important epoch of cosmic alignment.
6443 years ago, a quarter of the precessional cycle, in 4444 BC, the time of Carnac and the Boyne valley monuments, it was a spring equinox sun which lined up with the galactic centre, and 6443 years in the future it will be an autumn equinox sun which does the same.
10,260 years ago, a quarter of the obliquity cycle, in 8,200 BC, the builders of Gobekli Tepe were aligning their great T-shaped pillars on Orion, while experiencing the most northerly and southerly extreme summer and winter solstices for 41,000 years.
What the Mayan Long Count has finally revealed is that ancient astronomers were perfectly capable of understanding these long cycles and reducing them to fractional relationships, which are still highly relevant today.
It seems obvious from the evidence presented here that the ancients were accutely aware of the importance of some of these simple ratios, ratios which surround us, and yet which currently defy any scientific explanation.












A cosmic vision as if we have entered a field of high energy transmitting radiating frequencies of harmonic convergence covering and aligning with time once more.