Authors’ website: nazcasolution.com
Part I: The Nazca Great Circle Map Hypothesis
The lines and geoglyphs carved into the Nazca plateau represent a map of the Earth. The map is a Great Circle Map: a gnomonic projection with the center of the Earth as its cartographic view point. Each line on the Nazca Plateau represents a great circle of navigation centered at the center of the Earth and encircling the entire planet.
The majority of the lines on the Nazca Plateau radiate from five loci of origin called radial centers. The five radial centers are labeled C, A, T, G and R on the complete blueprint of the Nazca Map-Plateau as presented in Plate-1. Each radial center represents a specific geographic location on the surface of the Earth. The unicursal geoglyphs drawn amidst the straight lines function as eco-geographical markers—each figure representing a different geographic region of Earth. Using the geoglyphs as guides one can orient the Nazca map and infer the precise geographic locations of the radial centers on Earth. Once the exact radial center locations are known, the lines of the 2-Dimensional map-plateau can be projected as 3-dimensional great circles that circumscribe Earth.
To orient or key the Nazca map one begins with the geoglyph that depicts two llamas (Figure-1). The figure on the right of the llamas, often referred to as their “pen” or “corral”, will be addressed in a later work. The llamas suggests a clear and particular association with South America, specifically with the Andean region where the map itself is found. Therefore the llamas geoglyph is cartographically assigned as representing the Nazca-Andean region of Earth.

Picture-1 (PD0)
The nearest geoglyph eastward of the llamas is that of a spider-monkey seen in Picture-1 and Figure-2. The monkey appears hanging inverted from a jagged line formation that resembles a mountain chain, suggestive of the Andes mountains. This is geographically reasonable—as one moves eastward from Nazca over the Andes mountains one drops into the western Amazon Basin, where spider-monkeys abound. The spider-monkey glyph is therefore cartographically assigned to the southwestern region of the Amazon Basin.
Northward from the spider-monkey one finds the geoglyph called the grampus, or dolphin (Figure-3). The dolphin figure borders the southwestern edge of a large quadrangular polygon, labeled “Amazon River” on Plate-2.
One tends to associate dolphins with oceans, yet before one reaches the Caribbean Sea to the north of the Amazon, one encounters a particular and anomalous species of dolphin: the Amazon River Dolphin. These fresh water dolphins inhabit the western headwaters of the Amazon River.
Considered thus, the Amazon River Dolphin figure becomes a highly specific identifier for the Amazon River — the largest river of Earth—allowing one to infer that the large rectangular polygon adjacent to the river dolphin is a cartographic representation of the Amazon River itself. From this inference one may further infer that: all polygonal and triangular geometric shapes on the Nazca map are cartographic representations of rivers and water ways. The shallow tapering of the Amazon River Trapezoid towards its western end—is suggestive of the easterly flow of the Amazon River current—leading to an additional hypothesis: water currents flow in the direction of widening of polygonal or triangular figures.
Eastward from the river dolphin, towards the eastern end of the Amazon River Polygon is the figure of a downward diving fish (Figure-4). The downward orientation of the fish is suggestive of the Amazon River waters “falling” into the Atlantic Ocean. We therefore cartographically assign this fish to the Amazon River Delta region.
Directly beneath the easternmost end of the Amazon River quadrangle is the radial center labeled “A“ on Plate-2. The mouth of the Amazon River occurs at the terrestrial Equator—providing a “natural” cartographic location that allows one to infer the geographic location of the first radial center. The Amazon Radial Center (A) is therefore assigned equatorial coordinates at the center of the largest island in the Amazon River Delta: 0 North, 50 West.
Towards the northwest of the Amazon River radial center is the geoglyph of a hummingbird (Figure-5). These birds are unique to the Americas and exist in abundant numbers and variety in the Northern Amazon and Central American region, as indicated by the figure’s relative position in relation to the Amazon River.
Southward from the Amazon River is the figure often misidentified as a dog (Figure-6). The rounded ears and its inverted “hanging” orientation are strongly suggestive of a Tamandua, a semi-arboreal mammal that is unique to South America, inhabiting a vast range of forests and savannas south of the Amazon River (Picture-2).

Picture-2 ‘Tamandua mexicana’ by Dick Culbert (CC BY 2.0)
To the southeast of the Amazon River polygon is the geoglyphic figure often called a condor (Figure-7). From a biological standpoint the figure lacks all bird of prey characteristics. The beak and legs are too long and thin, not short and robust like a condor’s, and it lacks the large wing span in relation to the tail. The bird represented is actually a Willet—a coastal bird that ranges the Atlantic coasts from southern Brazil to the coasts northward of Florida (Picture-3). When viewed from above, flying low along the shore, Willets look very much as depicted by the geoglyph drawn on the plateau. Willets are unique to the eastern shorelines of the Americas, indicating that eastward from this point is the Atlantic Ocean.

Picture-3 ‘Willet’ by Andy Reago & Chrissy McClarren (CC BY 2.0)
Adjacent to the northeast of the willet and spanning eastward is a large polygonal shape labeled “ATLANTIC” (Plate-3). Applying the hypothesis that polygons and triangles represent water-ways, the large polygon must represent a portion of the Atlantic Ocean—from the easternmost shore of South America to the western shores of the African continent. The sub-hypothesis that water currents flow in the direction of polygonal widening finds congruency—the Atlantic South Equatorial Current flows westward from the Bight of Africa towards South America’s easternmost shore—as indicated by the Atlantic polygon widening towards the west.
Further eastward on the map, beyond the Atlantic polygon is the geoglyph often referred to as a lizard (Figure-8, Plate-4). The long narrow snout is more representative of a crocodile and of the Bight of Africa.
Towards the south of the crocodile in Plate-4 is the figure commonly referred to as a tree, seen in (Figure-9). The figure is drawn at the eastern end of a long thin triangle. Trees are not the only natural phenomena with “branching” morphology. Following the sub-hypothesis that the triangles and trapezoids represent waterways, and the fact that the figure in question is found at the end of a long narrow triangle, suggests that there is a unique element south of the Congo region and at the end of a water way with an eastward inland flow, as indicated by the triangle broadening towards the East.
The unique element in question must be the anomalous Okavango River Delta (Picture-4). The Okavango River and its delta are geographic anomalies—the Okavango River the only major river on Earth that flows inland, away from the sea to empty into the African savanna. As the only major river on Earth with an inland river delta—its uniqueness provides a highly specific geographic location. Even in our present day, from a high vantage over modern day Botswana, the Okavango River Delta bears an uncanny likeness to the delta geoglyph.
South of the Okavango Delta numerous lines converge at the easternmost radial center of the Nazca map, labelled “C” on Plate-5. Further south the figure of a Right Whale (Figure-10) suggests the Southern Ocean. The location of the radial center is therefore somewhere south of the Okavango River Delta yet north of the Southern Ocean—at the southern end of the African Continent.
The African continent reaches its southernmost geographic extreme at “Cape Agulhas”, Portuguese for “Cape Needles”. The topography of the cape narrows southward into a specific and precise geographic location (Picture-5). The Cape Agulhas Radial Center (C) is therefore assigned the coordinates at southernmost point of the African continent: 34.839 South, 20.004 East.
Having identified the easternmost radial center at Cape Agulhas, we return westward to the radial center composed of only three lines to form a triangle, as shown in Plate-6. The triangle’s location south of the Andean llamas may suggest that the radial center in question is within the South American continent or near its western shoreline. Yet its apparent location on Plate-1 in relation the Amazon River suggests a location a considerable distance to the southwest—in the South Pacific Ocean. The reason for the cartographic ambiguity in the location of figures will be addressed in a later work. There is in fact a very famous and rather anomalous island in the South Pacific Ocean with triangular topography—the island of Rapa-Nui, commonly known as Easter Island as seen in Picture-5.
Easter Island is considered one of the most geographically isolated islands on Earth—having wide expanses of ocean between itself and other shores. It is also the location of the anomalous cyclopean stone monuments known as Moai. The Rapa-Nui Radial Center (R) is therefore assigned a location at the geometric center of Easter Island: 27.109 South, 109.366 West.
To the northwest of Easter Island is the map’s westernmost radial center, labelled “G” on Plate-1. There are no geoglyphic figures in this part of the map to give eco-geographic clues to identify the radial center. Its general cartographic location far to the northwest of Easter Island, suggests perhaps a location in the vicinity of the Hawaiian Archipelago, such as its highest point at the volcanic summit of Mauna Kea. This would be a reasonable proposition in keeping with the theme of the anomalous extreme—measured from its base at the bottom of the ocean, Mauna Kea is the tallest mountain and largest shield volcano on Earth. Before settling on this conclusion, cartography itself provides yet another clue to infer the identity of the westernmost radial center.
The extremely long line labelled “Antipodal Orient” in Plate-1 and Plate-7 connects the easternmost radial center at Cape Agulhas with the westernmost radial center in question. This line is categorically different from other lines—connecting the two distal non-adjacent radial centers—suggesting an elementary cartographic relationship between them. Their positions at opposite ends of the primary grid indicate that the radial centers are Geodesic Antipodes—representing locations on exact opposite sides of the Earth. The antipode to Cape Agulhas is a point on the Pacific Ocean north of the Hawaiian Islands. The westernmost radial center is therefore assigned the geographic coordinates at the Geodesic Antipode to Cape Agulhas (G): 34.839 North, 159.996 West.
The lines that connect adjacent radial centers are called primary lines. The primary lines form the primary grid of the map and are drawn as wider lines on Plate-1. The primary lines are named and labelled according to the radial centers they connect: G-R, R-A and C-A. The primary lines represent primary great circles that can be projected into virtual orbital imagery as shown in Image-1, Image-2 and Image-3.
This primary grid of great circles is the key anchoring element of the Nazca map. The lines of the primary grid represent primary great circles that transect the geographic locations of the radial centers. The angular alignments of these primary great circles are geographically determined by the radial centers they transect.
The numerous other lines that radiate from the radial centers are called secondary lines. The secondary lines represent secondary great circles that are angularly aligned in relation to the primary great circles of the primary grid.
The Antipodal Orient great circle transects antipodal radial centers and is therefore not locked into a determined alignment. The Antipodal Orient great circle, as its name implies, follows the Orient Rule—the Antipodal Orient great circle is aligned to East-West at Cape Agulhas. It is a property of great circles to mirror angular alignment at any antipodal point—therefore the angular alignment of the Antipodal Orient great circle is also due East-West at the antipode (G) to Cape Agulhas. Before projecting the antipodal orient great circle, or any other secondary great circles of the map, we draw attention to the last radial center—at the central and capital position on the map—the radial center labelled “T” on Plate-1 and Plate-8.
Its central position on the map, to the south west of the Amazon River, suggests the vicinity of the Nazca Plateau itself. Yet not far from Nazca is another unique and monumental terrestrial anomaly—Lake Titicaca. Lake Titicaca is the highest lake on Earth and its salty water a remnant of its oceanic origins. On the shores of this anomalous and extreme lake are the ruins of the most elevated ancient megalithic structures—the ruins of Tiwanaku, the cradle of Andean civilization. The ruins are of enormous megalithic proportions and of great uncertain age. The Tiwanaku Radial Center is therefore assigned the geographic coordinate location of the largest central monument at the site—the Akapana Pyramid: 16.558 South, 69.657 West.
Upon close inspection the Tiwanaku radial center is categorically different from the other radial centers on the map—none of its lines directly connect to any other radial center. Tiwanaku is central and disconnected from the primary grid, implicating it as the Capital of the Nazca Map. Yet this lack of connection to a second radial center leaves no reference to geographically anchor the angular alignment of its many radiating great circles. The situation is similar to that of the Antipodal Orient requiring the Rule of Orient. One must infer which line of the Tiwanaku lines represents the great circle aligned towards Orient—due East-West—at Tiwanaku.
Here we call attention to yet another anomalous line labelled “Tiwanaku Parallel” seen on Plate-1 and Plate-8. The Tiwanaku Parallel is the longest line on the Nazca map-plateau. The Tiwanaku Parallel nearly transects the central Tiwanaku radial center, yet truly transects the Amazon radial center. This extreme long line cannot represent only a great circle from the Amazon radial center—for it continues far beyond it across the entire map. Any line that transects a radial center and radiates on its opposite side represents one same and single great circle. The cartographic anomaly of transecting the Amazon radial center and traversing the entire map-plateau suggests a cartographic meaning. The Tiwanaku Parallel line runs in perfect cartographic parallel with a Tiwanaku line labelled “Tiwanaku Orient ” shown in Plate-8. This cartographic paralleling of lines indicates the Tiwanaku Orient as the line that follows the Rule of Orient and represents a great circle that geographically anchors the Tiwanaku radial center. The Tiwanaku Orient Line represents a great circle that is angularly aligned to Orient—East-West—at Tiwanaku. All secondary great circles that radiate from Tiwanaku are angularly aligned in relation to the Tiwanaku Orient great circle. Since the Tiwanaku Parallel has a double function as a cartographic guide and as a secondary great circle from the Amazon radial center, it is labelled “A-2” at the Amazon radial center.
Having determined the three primary and Tiwanaku Orient great circles, one is ready to project all the great circles of the Nazca map. The method of angular measurement of secondary lines and their projection into great circles is graphically demonstrated in Plate-9, showing line C-1 measured in relation to primary line C-A and projected as a great circle in Image-4. The secondary lines from the other radial centers are similarly measured and projected in relation to the primary great circles. The method for each radial center is graphically demonstrated in the Data section of this work as well as numerical tables providing the angular alignments of all the Nazca lines and corresponding great circles.
Before projecting the complete array of Nazca map lines into great circles we call attention to a pattern along the path of primary great circle R-A. The course of primary great circle R-A traverses the coast of Peru and nearly transects the Nazca Plateau itself. Further discernment reveals that along the path of great circle R-A are the ruins of many famous ancient monumental structures, shown in Image-5 to Image-7.
The virtual imagery shows that the Nazca Plateau, Machu Picchu, Sacsayhuaman, the Giza Plateau, Petra, Ur and Eridu, Persepolis, Mohenjo-Daro, Angkor-Wat, and other ancient sites of great renown are in close geographic alignment with the great circle as its circles back to Easter Island and its ancient monolithic Moai. In summary: A significant number of cradles of civilization and ancient sites of great renown are found along the course of primary great circle circle R-A.
This “Cyclopean” Great Circle—named thus after the gigantic scale of masonry and structural ruins found along its course—was first noticed by a man named Jim Alison. Alison had noticed the cyclopean and many other great circle alignments from the empirical evidence provided by the geographic locations of the sites themselves. Such great circle alignments of ancient sites had previously been ignored, as had their profound historical implications. Alison found that sites of import were located at equidistant intervals of geometric significance along the course of the cyclopean great circle. Other investigators such as Robert Bauval and Graham Hancock had previously noted equidistant longitude relationships between ancient sites of note, echoing Jim Alison’s findings. Jim Alison had strongly suspected that Nazca—itself a site in the Cyclopean Great Circle Alignment—represented a diagram of the great circles alignments. Jim Alison was not only correct, but was himself directly involved in the development of this present work, which owes much to his insight and collaboration.
The purpose behind the great circle alignments of the ancient sites and the Nazca map becomes clearer when the other phenomena under the great circles are discerned: Impact craters and volcanic calderas. These two “cataclysmic” categories of phenomena are also in great circle alignment with the great circles of the Nazca map. A fourth category of submerged monuments includes submerged archeological sites of recent discovery or rumor that are found suggestively near the courses of the great circles of the Nazca map. The complete site list of all ancient monuments, volcanoes and impact craters and their geographic coordinates are provided in the Tables section of this work.
We are now ready to project all the great circles of the map and all the ancient monuments, volcanoes and impact craters in virtual imagery. After their presentation all the great circle alignments that are to be scientific tested and analyzed in the next section of this work.
The great circles from each radial center are virtually projected in different colors for visual differentiation:
Primary great circles: red;
Tiwanaku great circles: white;
Cape Agulhas great circles: green;
Amazon great circles; yellow;
Geodetic Antipode great circles: orange.
Tiwanaku Orient great circle: dark grey
Antipodal Orient great circle: black.
Easter Island great circle(single): purple.
The different categories of sites are also projected in different colors for visual differentiation:
Monuments: black
Volcanoes: gold
Impact craters: red
submerged monuments: black / aquamarine center
The virtual orbital imagery in Image-8 to Image-18 shows all the great circles of the Nazca Great Circle Map and the ancient monuments, major volcanoes and impact craters in its global construct, projected on the virtual Earth.
Part II: The Random Simulation Experiment – A Statistical Analysis of The Nazca Great Circle Map-Plateau
To prove that the Nazca Lines represent a great circle map that draws attention to volcanoes, impact craters and ancient monuments, one must design a unique scientific experiment. The goal of the experiment is to test for geographic correlation between the phenomena and the great circles proposed by the Nazca Great Circle Map Hypothesis. To do this one must gauge the correlation between the phenomena and the Nazca great circles and compare it to the correlation between the same phenomena and “random” great circles. By comparing the great circles alignments of the Nazca map with the great circle alignments that result from a randomized version of the map, one can scientifically test the validity of the Nazca Map Hypothesis.
In statistical terminology the random version of the Nazca Map Hypothesis is called the “Null Hypothesis”, and the Nazca Map Hypothesis is called the “Alternative Hypothesis“. The Null hypothesis is the anti-hypothesis that assumes that the Nazca Map Hypothesis is not true. The Null Hypothesis states: “There is no relationship between the sites and the great circles proposed by the Nazca Map Hypothesis. The great circle alignments observed are as likely to occur by random great circle patterns”.
In order for the Nazca Map Hypothesis to be accepted as “true”, the Null Hypothesis must be rejected as “false”. The Null Hypothesis experiment can be said to be the experiment that shows the results of random chance. If the Null Hypothesis experiment results show that the great circle alignments proposed by the Nazca Map Hypothesis are statistically “unlikely” to result from random chance, then Nazca Map Hypothesis must be accepted as true.
Such an experiment that can compare random great circle patterns with those proposed by the Nazca Map Hypothesis can be achieved with a computer program, or computer simulation. The program simulates a virtual Earth with its ancient monuments, volcanoes and impact craters at their exact latitude and longitude locations. The simulation then generates radial centers at random locations on the virtual Earth, with great circles that radiate from them at random angles, or headings.
The Random Simulation program generates a perfectly randomized version of the Nazca Map Hypothesis that can be repeated like any testable and verifiable scientific experiment. The great circle alignments of the random simulation can then be compared with the great circle alignments of the Nazca Map Hypothesis to answer the following question: What is the probability that 79 “randomly” aligned great circles will geographically correlate with as many phenomena as those that result from the Nazca Map Hypothesis?
Before moving on to the Random Simulation experiment some important concepts and terms must be elaborated and defined.
GREAT CIRCLE BANDWIDTH AND SITE DISTRIBUTION
A great circle alignment is the geographic correlation between specific sites, or locations, and the course of a great circle on the spherical surface of Earth. This geographic correlation is measured and analyzed in reference to the distance of the sites in question to the path of the great circle. If one imagines each great circle as an infinitely thin geometric line encircling Earth, the great circle could be said to encompass, or transect only locations that fall precisely in its path. Due to the large scale and numerous sites involved in the global construct, it would be unreasonable to expect precise linear transections of sites, since the number of phenomena far exceeds the number of great circles proposed by the hypothesis. The Nazca Map Hypothesis claims that each great circle has multiple sites in great circle alignment. The global map construct is of a “Best Fit Line” design similar to the Statistical concept of the “Linear Regression Line” as shown in Diagram-1.
As can be seen in the diagram, several of the points are precisely transected by the thin dark line. Yet the correlation, or association between the line and the other points is evident, and the points are said to be scattered about the line. To draw the analogy with the Nazca Map: the “points” are the Site locations of ancient monuments, volcanoes and impact craters and the “line” is analogous to the path of a great circle that circumscribes Earth.
To understand the correlation between the sites and the great circles it becomes useful to visualize each great circle as a great circle “band” having width, or bandwidth as shown in Diagram-1, which shows many more points being encompassed, or transected by the wider grey line. Each great circle band can likewise be visualized as encompassing multiple sites along its course. An example of great circles encompassing (transecting) more sites as they increase in bandwidth. can seen in the comparison between Image-19 and Image-20, which show the same Nazca great circles projected at different widths.
Any comparison of great circle correlation becomes self limiting at the opposite extremes of bandwidth. If the test bandwidth is extremely narrow neither random great circles nor those proposed by the Nazca Map Hypothesis will encompass any of the sites, nullifying any comparison of great circle correlation. The finite surface area of Earth sets an upper limit to great circle bandwidth. If the great circle bandwidth is wide enough such that 79 random great circle bands cover the entire terrestrial surface, both the random great circles and those of the Nazca map would encompass all the site locations on Earth nullifying any great circle alignment comparison.
The finite spherical surface of Earth also sets a theoretical limit on the geographic distribution of the sites being tested. This limit is best illustrated by its most extreme example: that of an Earth uniformly and completely covered in sites that are equidistant from each other. In such a case any great circle, regardless of its spatial alignment, will encompass the same number of sites, again nullifying any comparison test between random great circles and those proposed by the map hypothesis. Fortunately, the combined total number and geographic distribution of all the sites tested by the random simulation are not extreme enough to induce this “crowded Earth” effect and allowing the simulation yields significant comparative results.
SITE CATEGORIES
The term “site” is used in this work in reference to any location of interest for testing geographic correlation with the great circles of the Nazca map and with random great circles. Three principal categories of sites are tested for great circle alignments with the global construct of the Nazca map: Volcanoes, Impact Craters and Ancient Monuments. The Random Simulation program can perform great circle alignment tests on any of these categories individually or in combination.
Monuments
The monument category is an amalgam of anomalous and extreme structural sites of great age, magnanimity and civilizational import. The Nazca Great Circle Map suggests that the ancient monuments were constructed at specific locations on Earth in order to intentionally generate geographic correlation with the great circles of the map. This implies that the monuments and cradle cities were purposefully placed in order to cartographically reinforce the great circles of the map, and draw attention to the volcanoes and impact craters. The global construct of monuments is therefore a cartographic element of the Nazca Great Circle Map; a map whose primary subject is the natural phenomena of Earth.
Many of the monumental sites in the Nazca global construct are part of large structural complexes that were often ancient centers, or cradles, of civilization. The geographic placement of ancient monuments and cities is somewhat locally limited by the terrain and structural needs of each construction – such as stable ground foundations for extremely heavy monuments, the proximity of water sources for cradle cities and other geographic considerations. The global scale of the great circle construct allows for monuments and cradle cities to be placed at cartographic locations that nonetheless reinforce the great circles of the Nazca map. The monumental category can be further divided into sub-categories: monuments, geoglyphic monuments and submerged monuments. The geoglyphic category consists of “graphical” constructs that are either carved into, or formed from the terrain. Nazca, being the most monumental geoglyphic site on Earth as well as the blueprint of the global construct, is categorized as a monument in this work.
The submerged monuments category consists of a growing list of intriguing undersea structures representing the remains of past civilization. Unlike the land monuments, which were geographically placed to reinforce the map; the submerged monuments, like the volcanoes and the impact craters, were the intentional targets of the original great circle alignment.
An additional category of sites called “Other“, contains certain structural and natural phenomena and locations of mytho-historical interest. Some are archeological sites suspected to be locations mentioned in ancient mythology, others are natural phenomena that are central to a particular mythology – such as Mt. Olympus, or Uluru.
Volcanoes
The term “volcano” is a very broad categorization requiring finer definition. If one were to consider every lava vent on Earth to be a volcano, these would be so numerous and broad in geographic distribution as to induce the crowded Earth effect previously mentioned, nullifying the test. It is logical to expect that the mapmakers would intend to draw attention to the more anomalous and extreme volcanoes of great eruptive power and global climatic significance.
Establishing the eruptive power and catastrophic potential of a volcano is a complex matter. In some cases the eruptive power has been calculated from the remnant signs of past eruptions. The true measure of the eruptive power and potential global climatic effect of a volcano involves the volume, viscosity and chemical composition of the lava in its magma chamber. The general correlation between the volume of the magma chamber and the volume of the mountain-volcano itself, makes volume an ideal attribute for determining the volcano population to be tested. Yet the current scarcity of volcanic volumetric databases leaves “height” as the only practical attribute by which to estimate volume and define the test population for the experiment. The height of a mountain or volcano can be measured in two ways: topographic elevation and topographic prominence. The peak elevation of a mountain is its altitude above sea level, while its peak prominence is its height as measured from its base. A relatively small volcano rising from the top of a high continental massif may present a high elevation from sea level, yet have little eruptive power and global consequence. Peak prominence is the therefore a better indicator of the volume and power of a volcano, and is therefore chosen as the inclusion parameter for the great circle alignment test. The established geophysical category known as “Ultra-Prominent” constitutes volcanoes with peak prominences exceeding 1500 meters. The Ultra category of volcanoes is a clear, established and well defined geophysical category—a suitable and defined population for statistical testing.
An additional subcategory of volcanoes included in the experiment data set are the 16 volcanoes called “Decade Volcanoes“, by the International Association of Volcanology and Chemistry of the Earths’s Interior (IAVCEI). This list is comprised of volcanoes known to be regularly destructive or of particular scientific interest. It is worthy of note that many of these Decade Volcanoes are also Ultra volcanoes.
Volcanoes are indeed categorically different from monuments and cities—Nature alone determines their geographic locations. Yet these natural phenomena are not necessarily found in a “random” geographic distribution and under careful inspection certain geographic patterns become readily apparent. Mountain ranges are often associated with tectonic plate boundaries and exhibit the same linear tendency in their geography. It is along these plate boundaries and mountain chains that the majority of the Earth’s volcanoes are found. The linear geography inherent to mountain ranges results in volcanic belts: linear chains of volcanoes that allow for a single great circle to encompass multiple volcanoes. An example of such a volcanic belt is seen in Image-21, showing the Antipodal Orient great circle (black) encompassing beneath its course the linear belt of volcanoes (gold dots) that ridge the Central American Isthmus. The mapmakers made use of the natural linear tendency in volcanic geography to align the great circles of the Nazca map and thus draw maximum attention to these natural phenomena.
Impact Craters
Impact craters are the remnant lithospheric scars of cometary or meteoric impacts. The 189 (at the time of writing) currently accepted impact craters accepted in the field of Geophysics provides a well defined and established population for experimental testing. The general correlation between impact crater diameter and impact force allows for selection of crater populations of varying diameter, representing different levels of planetary climatic effect and significance.
Impact Craters present a more random geographic distribution than volcanoes. Their scattered random distribution is intermittently interrupted by crater “clusters” in certain regions of Earth. An example of such a cluster is seen (red dots) in the densely cratered region of Northern Europe around Scandinavia, shown previously in Image-19 and Image-20, or the densely cratered continent of Australia seen in Image-16 of the hypothesis section (Part 1). The Nazca great circles seen transecting the crater cluster exemplify how great circles can be aligned to encompass multiple impact craters beneath their courses, enhancing the best fit pattern and drawing attention to these phenomena.
Volcanoes and impact craters abide by other geographic patterns that are implied by the Nazca map and the global construct it illustrates. These geographic patterns suggest great geophysical import and will be addressed in a following section, after the Random Simulation puts the Nazca Great Circle Map Hypothesis through its scientific test.
THE RANDOM SIMULATION
The Random Simulation is a JavaScript computer program that runs on any modern Web Browser. An updated version with an improved interface will be available for anyone to run on nazcasolution.com and to download for anyone who wishes to inspect the code and mathematical calculations.
The Random Simulation uses two main data sets to perform its calculations: the Great Circle Data Set and the Site Data Set.
The Great Circle Set
Once the program is active it displays a series of boxes as seen in Picture-6. The box titled “Nazca Parameters” lists the latitude and longitudes of the five Nazca Radial Centers (RCs) and the number of great circles (CGs) that radiate from each. These parameters represent the data of the Nazca great circle map which are provided in Table-8 in the Data section along with the angles of each line on the plateau relative to its anchoring primary line and the true headings of their corresponding great circles. The Nazca parameters are a part of the simulation program and are not user alterable.
The small box titled “Settings” contains the input parameters the user can interactively change. The first input box titled “number of runs“, is the number of times the random version of the great circle map is to be simulated in the trial. Each run represents one cast of 79 randomized great circles. The default is set at 10,000 runs per trial. The higher this number off runs in an experimental trial, the longer the experiment run time, but the more statistically accurate the results yielded.
In each run the simulation generates four radial centers at random coordinates on the virtual Earth, with a fifth radial center at the antipode of one of these. The simulation then generates 79 great circles that radiate from these five radial centers at random angles, or headings. Each “run” thus represents one “random instance”, or random version of the great circles pattern of the Nazca map. The results of each trial forms a Bell Curve for statistical comparison of the pattern of chance with the pattern of the Nazca map. The greater the number of runs simulated per trial, the more complete the Bell Curve that forms from the results. From the Bell Curve produced by the results one can calculate the statistical probability of “random chance” resulting in great circle alignments comparable to those of the Nazca map. The greater the number of runs in a trial, the more statistically confident one can be in the calculated probability of random occurrence.
The input parameter, “Bandwidth” is the width of each great circle band in kilometers. This bandwidth applies to both the Nazca great circles and their random counterparts. If one inputs a 20 kilometer bandwidth the simulation will make each of the 79 Nazca great circles into bands 20 kilometers in width, and count the number of sites they encompass. The simulation then assigns the same 20 kilometer width to each great circle in the randomly generated sets of 79 and counts the number of sites encompass in each random iteration.
The Site Set
The large scrollable box labeled “Sites“, lists the monuments, volcanoes and impact craters available for the random simulation test and their latitude and longitude coordinates. Each site has a check box for individual inclusion or exclusion from the test. The sites appear on the list in order by category.
Ancient monuments and cities are listed first in alphabetical order. This list of ancient monuments and their coordinates is also provided in Table-5 in the Data section. There are several subtypes of monuments that are grouped together under categorical labels such as, “Pyramid“, “Menhir” or “Dolmen” in order to facilitate locating them on the list. There are exceptions to this grouping such as the Great Pyramid of Giza which is found alphabetically under letter “G” and not with the other pyramids.
The monument names which are written in capital letters represent those that serve as capitals of their monumental groupings. The capital groups are defined by a 50 kilometer radius from the capital monument and between satellite monuments in the group. If a monument is within 50 kilometers of a monument that is within 50 kms of a capital monument, both satellite monuments belong to that capital group. Therefore, if a monument is 50 kms or more from a capital monument or any of its satellites, it does not belong to any group and is considered a lone monumental site. All the monuments that are in the immediate vicinity of the Giza Plateau, for example, are part of the “Giza” group. This allows one to select the Great Pyramid as the single representative of the entire Giza group that would otherwise include the other many pyramids and monuments of the Nile Delta region. One can thus test entire groups or only the “Capital” monument of each group. The capital of a monumental group is, as best determined, the most anomalous or extreme structure of the group, as best determined. At the end of the monuments list is comprised of the subcategories, “Geoglyph”, “Submerged Monuments” and “Other”, followed by the impact craters as seen in Picture-7.
The currently accepted impact craters are numbered in order according to crater diameter to facilitate selection of test populations in terms of impact force and global climatic effect. The impact craters list with their coordinate locations, diameters, approximate ages and force of impact if available are also provided in Table-7 in Data section.
The volcanoes of Earth comprise the end of the site list and are grouped according to the continental plate on which they are found. Within each continental grouping the volcanoes are roughly in order by decreasing topographic elevation, not according to topographic prominence. The “Ultra” volcanoes with a topographic prominence exceeding 1,500 meters are in their respective continental plate groups in capital lettering for easy identification. The list of volcanoes with their coordinates, topographic elevation, topographic prominence and Volcanic Explosive Indexes (VEIs) is provided in Table-6.
The box labeled “Selections” allows the user to select and deselect entire categories and subcategories of sites to facilitate management of the list. All monument groups and capitals combined into a group, are available for selection. The impact crater selections constitute divisions at different crater diameter by “tens” of kilometers groupings. The volcanic subcategories “ULTRA” and “DECADE“, as well as by continental plates groupings, all are available as selections to customize the random simulation test.
Results Output
Once the great circle parameters and sites have been set the random simulation is ready to run. The box labeled “Results” seen in Picture-8 the output boxes for various numerical results and the simulation “Run!” button. The empty window within the box is where the results of each run are outputted. Each number is the total number of “Hits“, or sites encompassed by the 79 random great circles in one simulation run. If the trial consists of 10,000 runs, 10,000 results will be displayed in the scrollable box at completion.
Below the results box a series of output boxes display the results of the following statistical calculations:
Sum Total: The sum of the hits of all run results in the trial.
Mean: The statistical mean, or average of the total number of “Hits” (sites encompassed) for all run results.
Max: The maximum number of sites encompassed by a single simulated run in the trial.
Min: The minimum number of sites encompassed by a single simulated run in the trial. At the great circle bandwidths and number of runs per trial that are adequate for the test, this minimum tends to remain zero—at least one cast of random great circles not encompassing any sites.
Variance: The statistical Variance of the results of all runs in that trial. Also known as “Sigma Squared”.
Nazca Hits: The total number of sites encompassed (transected) by the great circles of the map at the bandwidth being tested.
CDF: The Cumulative Distribution Function result is the calculated Probability of Random Occurrence, or the probability that random chance has of achieving the same results as the Nazca Great Circle Map Hypothesis.
In addition to these numerical results the random simulation graphically displays a Distribution Curve of the results, seen also in Picture-8. The X-Axis of the curve is the discrete number of possible encompassed sites, or “Hits”; the Y-Axis is the total count of random runs that resulted in that number of encompassed sites. The distribution curve displayed is cursor-interactive; numerically displaying the number of runs for each “Hit ” value at the lower left corner of the Distribution Curve window.
As previously mentioned, the Random Simulation yields the results of each trial in a the Results box along with a distribution curve as seen previously in Picture-8, which shows a well defined distribution curve.
At narrow great circle bandwidths of only a few kilometers, few sites are encompassed and the distribution curve is therefore incomplete, as can be seen in Picture-9, which shows the results and distribution curve from a test trial on all impact craters at 1 kilometer great circle bandwidth. The incomplete “half-bell” shape of the distribution curve is due to the fact that at narrow great circle bandwidths there are many random great circle sets that yield “Zero Hits“—no sites being encompassed, or transected by any of the randomized great circles.
The Cumulative Distribution Function (CDF) requires a complete distribution curve to accurately calculate the probability of random occurrence. The probability results of the simulation are therefore not valid at very narrow great circle bandwidths. As one increases the width of the great circles the simulation results in less instances of “zero hit” runs and a complete distribution curve begins to form. Picture-10 shows a complete distribution curve begin to form at around 8 kilometers of great circle bandwidth for the impact craters trial. It is at this great circle width, or greater, that one may have statistical confidence in the results for that particular category of sites (all impact craters). The specific bandwidth at which a complete distribution curve forms varies with site category being tested, yet all categories show a clear distribution curve forming by a great circle bandwidths of 8 kilometers.
THE NULL HYPOTHESIS EXPERIMENT
The Random Simulation provides the experimental data for the statistically analysis of the Nazca Great Circle Map Hypothesis. The initial experiment entails a complete scan of great circle bandwidth on the following four site categories: 1. Monuments, 2. Volcanoes, 3. Impact Craters, and 4. All three categories combined.
This initial experiment excludes the subcategories of monument sites: submerged sites, geoglyphic sites (with the exception of the Nazca Geoglyphic Monument itself), and the category “OTHER”. These excluded subcategories are available for selection in the simulation for any user to test individually or in combination. A few new monuments have been added to the list since this experiment. These additions only improve the result. The population tested for the experiment were the Capital Monuments of each monument group and those not satellites of a monument group (non-satellite monuments). The volcanoes tested were are all those belonging to the “Ultra” and “Decade” categories. All impact craters accepted in the field of Geology were included in the experiment.
Each experimental trial consisted of 100,000 runs, or 100,000 random map iterations, at each bandwidth tested. This number of runs was determined, through trial and error, to balance statistical accuracy of the results with computation times. At 100,000 runs per trial there is very little variance in the trial results and these produce well-defined Distribution Curves that allow the Cumulative Distribution Function (CDF) to yield accurate calculations of the probability of random occurrence.
In order to reduce computation times each scan begins at 1 kilometer great circle bandwidth, then 5 kms, then 10 kms and increasing by 10 kilometer increments each trial thereon. The 10 kilometer increments allow the scan of the entire range without the thwarting computation times involved in doing all 1 km increments. However, in the attempt to precisely locate the great circle bandwidth at which the exact maximum(s) occurs, several spans of the scans are in 1 kilometer increments. In the future we hope to provide complete 1km resolution for all data—until such a time a user may test the Random Simulation at any missing great circle bandwidth in question, or use it to verify the results of the experimental presented below.
RESULTS ANALYSIS
The complete results of the Random Simulation scans are provided in Table-1 thru Table-4 in the Data section, where the experiment results for the monumental, volcanic, impact crater and all categories combined are tabulated. The right side columns of the tables give the probability of random occurrence and can be seen to vary with both great circle bandwidth and between site category—each category peaking in probability by different amounts and at different great circle bandwidths.
In statistical analysis “statistical significance” is the point at which the probability of an event occurring randomly is considered to be sufficiently unlikely for rejecting the Null Hypothesis and accepting the Alternative Hypothesis. This significance level is often set at .05 (5%) or .01 (1%). This is to mean: If random chance reproduces the effect less than once in twenty, or less than once in one hundred times, the Alternative Hypothesis (Nazca Map Hypothesis), must be statistically accepted as true.
The probability of occurrence of great circle alignments shown by this experiment is far above the threshold acceptance level for each category of sites, within a broad range of great circle bandwidths.
To help visualize the data, graphs of the probability of random occurrence according to great circle bandwidth for monuments, volcanoes, impact craters and all three categories combined, are presented below.
The horizontal axis of the graphs represent great circle bandwidth in kilometers. Since the Continuous Distribution Function (CDF) yields results as decimals, the graph plots 1 / CDF, to represent the Probability of Random Occurrence and avoid graphing a decimal on the Y-axis. The higher the probability peak on the Y-axis of the graph, the less likely that the Nazca great circle alignments could be the result of random chance for great circles of that bandwidth.
The first graph for the ancient monument category shows a peak at 40 kilometers great circle width with a probability of random occurrence of 2112—the random great circles only achieving geographic correlation with monuments, equivalent to the Nazca map’s great circle alignments, only once in 2112 random iterations. This is 100 times greater than required for statistically significance. The strength of correlation is evidence of the monuments being in purposeful great circle alignment with great circles of the Nazca map.
The second graph shows the result for the volcanic category. The peak occurs at 28 kilometers great circle bandwidth, with a probability of random occurrence of once in 612 random iterations; 6 times greater than required for statistical significance.
The last graph shows the results for the impact crater category. The peak occurs at 1 kilometer greats circle width and a probability of random occurrence of once in 161 random iterations. As previously mentioned, however, the distribution curve is incomplete until about 8 kilometers of great circle width. We therefore consider 8 kilometer great circle width to be the start of statistical confidence. The maximum is therefore at 9 kilometers great circle width and probability of random occurrence of once in 37 random iterations. This is still nearly twice the generally accepted, ” once in 20 “, minimum threshold. This is clear evidence of correlation with the great circles of the Nazca map, but not as strong as the other two categories. The lack of both natural and artificial linearity in the geographic distribution of impact craters—their geographic randomness—is the likely explanation. Volcanoes, having more geologic linearity, are more easily incorporated into great circle alignments, snd the monuments are purposefully placed in order to reinforce the the great circle alignments.
The last graph shows the results for the monuments, volcanoes and impact craters combined category. At a great circle bandwidth of 29 kilometers the probability of random occurrence is once in 42,028 random iterations…. 420 times the required statistical threshold.
The fact that all categories combined reaches a probability of random occurrence far greater than any individual category constitutes overwhelming evidence that all the categories have great circle alignment with the great circles of the Nazca Map.
This initial experiment does not take into account triangulation or hierarchy. In other words, it does not test for the fact that in many cases the larger volcanoes and impact craters are “triangulated”, or transected, by more than one great circle. An example of this prioritizing can be seen in Image-21, where the third largest known meteor crater (red dot) Chicxulub – nemesis of the dinosaurs -is triangulated by two Nazca map great circles at the tip of the Yucatan Peninsula. A volcanic example of the same principle is seen in Image-22, showing the triple great circle transection of Mount Kerinci—largest volcano in Sumatra and one of the largest on Earth. Random simulation tests that include multiple transections upon single sites will be run and added to this work in the near future.
It is worth noting that the ancient monuments for testing by the random simulation experiment are a broad population in an attempt at being inclusive and non biased. In other words, the list of monuments gives the Null Hypothesis the advantage. It is a fact that if one selected only the sites known to be encompassed by the great circles the experiment would retain scientific and statistical validity—the Random Simulation would still calculate an accurate probability of occurrence of even greater statistical significance.
CONCLUSION
The Nazca Great Circle Map Hypothesis, as tested by the Random Simulation program, yields overwhelming statistical evidence of being true. The geographic correlation of ancient monuments, volcanoes and impact craters with the great circles of the Nazca map is statistically unarguable.
The empirical evidence in the form of newly discovered accepted impact craters and ancient monuments will continue to strengthen the proof presented here. In fact, we encourage all people to use the Nazca great circle map to assist in the rediscovery of our past, and all that remains hidden in Earth’s majesty.
DATA
Table-1: Monumental Category Random Simulation Results
|
Great Circle |
Nazca Map |
Mean |
Max |
Variance |
CDF |
Prob. of Random |
|
Width (Kms) |
Transects |
Random |
Random |
Occurrence (1/CDF) |
||
|
1 |
1 |
1.02117 |
8 |
1.065102 |
0.5081828785 |
1.967795536 |
|
5 |
10 |
5.05436 |
23 |
6.146025 |
0.02302583716 |
43.42947416 |
|
10 |
16 |
10.05015 |
34 |
13.964595 |
0.05567226352 |
17.96226589 |
|
15 |
22 |
14.94994 |
48 |
23.140274 |
0.07138181693 |
14.00916988 |
|
20 |
30 |
19.79984 |
55 |
33.873076 |
0.0398364322 |
25.10264963 |
|
25 |
40 |
24.58318 |
66 |
44.752521 |
0.01059590645 |
94.37606916 |
|
26 |
42 |
25.55066 |
66 |
47.158674 |
0.008302414272 |
120.4468926 |
|
27 |
46 |
26.52405 |
69 |
50.044822 |
0.002951859247 |
338.7695403 |
|
28 |
47 |
27.45412 |
77 |
52.057455 |
0.003374015161 |
296.382782 |
|
29 |
49 |
28.40861 |
70 |
54.694328 |
0.002682249567 |
372.8213856 |
|
30 |
51 |
29.34177 |
72 |
57.410663 |
0.002128754118 |
469.7583397 |
|
31 |
52 |
30.31206 |
77 |
60.033299 |
0.002562069602 |
390.3094589 |
|
32 |
53 |
31.2058 |
80 |
62.383526 |
0.002895869506 |
345.3194275 |
|
33 |
54 |
32.12268 |
80 |
64.82677 |
0.003292131537 |
303.7545702 |
|
34 |
57 |
33.08361 |
84 |
67.591259 |
0.00181267657 |
551.6703953 |
|
35 |
59 |
34.01746 |
81 |
70.436815 |
0.001456790543 |
686.4404803 |
|
36 |
60 |
34.9362 |
86 |
72.91023 |
0.001666119912 |
600.1968963 |
|
37 |
61 |
35.96296 |
87 |
75.687908 |
0.002001911018 |
499.5227016 |
|
38 |
63 |
36.83956 |
90 |
78.085459 |
0.001535874147 |
651.0950145 |
|
39 |
65 |
37.73091 |
90 |
80.825121 |
0.001209976229 |
826.4625172 |
|
40 |
69 |
38.6493 |
91 |
84.28515 |
0.000473314772 |
2112.758906 |
|
41 |
69 |
39.57325 |
92 |
87.174274 |
0.000811549119 |
1232.211306 |
|
42 |
69 |
40.52519 |
100 |
89.741445 |
0.001324288495 |
755.1224705 |
|
43 |
71 |
41.42047 |
104 |
92.301835 |
0.001039066504 |
962.4023064 |
|
45 |
72 |
43.25039 |
101 |
98.466695 |
0.001882195946 |
531.2943119 |
|
50 |
75 |
47.80773 |
109 |
113.940582 |
0.005425617128 |
184.3108307 |
|
55 |
80 |
52.2583 |
111 |
127.849121 |
0.007073883722 |
141.3650605 |
|
60 |
86 |
56.70239 |
122 |
143.206298 |
0.007178120057 |
139.3122422 |
|
70 |
100 |
65.52776 |
132 |
177.307389 |
0.004814918106 |
207.6878522 |
|
80 |
112 |
74.03965 |
153 |
207.270258 |
0.004185766991 |
238.9048416 |
|
90 |
129 |
82.52369 |
163 |
239.173399 |
0.001326976378 |
753.5929174 |
|
95 |
135 |
86.56765 |
170 |
258.085703 |
0.00128588917 |
777.671998 |
|
96 |
139 |
87.50512 |
177 |
261.726134 |
0.000728716781 |
1372.275246 |
|
97 |
141 |
88.2559 |
174 |
264.803115 |
0.00059503681 |
1680.5683 |
|
98 |
142 |
89.05034 |
172 |
270.952386 |
0.00064826808 |
1542.571709 |
|
99 |
144 |
89.93731 |
177 |
275.9765 |
0.000568300706 |
1759.63181 |
|
100 |
145 |
90.80907 |
180 |
276.470356 |
0.000558762887 |
1789.667895 |
|
101 |
145 |
91.66319 |
174 |
278.915689 |
0.000702373611 |
1423.743695 |
|
102 |
145 |
92.45056 |
168 |
282.631536 |
0.000886684413 |
1127.796976 |
|
103 |
147 |
93.24157 |
182 |
288.557414 |
0.000776255282 |
1288.236001 |
|
104 |
147 |
94.00979 |
180 |
291.370714 |
0.000953441684 |
1048.831844 |
|
105 |
148 |
94.89148 |
181 |
295.227043 |
0.00099772606 |
1002.279123 |
|
110 |
154 |
98.87309 |
183 |
310.885484 |
0.000884394405 |
1130.717239 |
|
111 |
155 |
99.7239 |
185 |
315.047309 |
0.00092215475 |
1084.416688 |
|
112 |
157 |
100.61823 |
199 |
318.859262 |
0.000795723998 |
1256.717156 |
|
113 |
158 |
101.30142 |
192 |
321.355606 |
0.000781151455 |
1280.161476 |
|
114 |
159 |
102.08883 |
191 |
323.749699 |
0.000780886027 |
1280.596611 |
|
115 |
160 |
102.91424 |
194 |
331.526345 |
0.000858610706 |
1164.672177 |
|
120 |
163 |
106.86447 |
194 |
344.326202 |
0.001242381067 |
804.90602 |
|
130 |
174 |
114.78037 |
208 |
379.878153 |
0.001189229289 |
840.8807362 |
|
140 |
183 |
122.37565 |
217 |
412.194277 |
0.001413062672 |
707.6826951 |
|
150 |
188 |
129.98368 |
228 |
447.046494 |
0.003035377107 |
329.4483567 |
|
160 |
197 |
137.53499 |
242 |
486.315496 |
0.003503488017 |
285.4298331 |
|
170 |
203 |
145.00025 |
248 |
515.69263 |
0.005323784325 |
187.8363095 |
|
180 |
211 |
152.08705 |
269 |
548.807932 |
0.005955276812 |
167.918307 |
|
190 |
215 |
159.37151 |
266 |
585.49373 |
0.01075289324 |
92.99822638 |
|
200 |
223 |
166.00976 |
276 |
615.751545 |
0.01081893095 |
92.43057418 |
|
210 |
227 |
173.16618 |
290 |
647.696024 |
0.01720268676 |
58.13045451 |
|
220 |
236 |
179.82913 |
292 |
684.907233 |
0.01592356911 |
62.79999121 |
|
230 |
242 |
186.61424 |
306 |
713.384989 |
0.01905576134 |
52.47756741 |
|
240 |
247 |
193.24783 |
311 |
743.45985 |
0.02434101669 |
41.08291829 |
|
250 |
252 |
199.51142 |
320 |
770.38527 |
0.02930655829 |
34.12205521 |
|
260 |
257 |
206.17046 |
338 |
797.460283 |
0.03593386954 |
27.82889828 |
|
270 |
264 |
212.33561 |
338 |
825.596916 |
0.03608273244 |
27.71408739 |
|
280 |
269 |
218.58519 |
349 |
860.947243 |
0.04288145728 |
23.32010299 |
|
290 |
280 |
224.72634 |
345 |
874.20547 |
0.03078082995 |
32.48775299 |
|
300 |
285 |
230.56728 |
363 |
900.570613 |
0.03485047906 |
28.69401015 |
|
310 |
292 |
236.54587 |
365 |
937.834216 |
0.03508578521 |
28.50157105 |
|
320 |
297 |
242.51655 |
371 |
954.029726 |
0.03887109384 |
25.72605762 |
|
330 |
302 |
248.15849 |
387 |
986.530291 |
0.04324580705 |
23.12362905 |
|
340 |
308 |
253.85356 |
387 |
1006.156715 |
0.0439097195 |
22.77400109 |
|
350 |
317 |
259.27308 |
387 |
1029.225247 |
0.03597920088 |
27.79383576 |
|
360 |
318 |
264.80199 |
402 |
1056.194722 |
0.05082519261 |
19.67528205 |
|
370 |
321 |
270.47386 |
404 |
1083.241617 |
0.06237234942 |
16.03274543 |
|
380 |
331 |
275.90581 |
408 |
1100.734938 |
0.04839713609 |
20.66237965 |
|
390 |
336 |
281.08383 |
417 |
1116.950463 |
0.05017357297 |
19.930811 |
|
400 |
345 |
286.34046 |
439 |
1138.189527 |
0.04104140838 |
24.36563557 |
|
410 |
350 |
291.47928 |
443 |
1161.900531 |
0.04300587835 |
23.25263518 |
|
420 |
354 |
296.43749 |
435 |
1173.99149 |
0.04647942138 |
21.51489778 |
|
430 |
358 |
301.63634 |
443 |
1189.244591 |
0.05108537366 |
19.57507459 |
|
440 |
363 |
306.61545 |
454 |
1216.526131 |
0.05298360192 |
18.87376403 |
|
450 |
366 |
311.44839 |
456 |
1233.742836 |
0.06020140348 |
16.61090842 |
|
460 |
373 |
316.33507 |
457 |
1256.927218 |
0.05498770683 |
18.18588295 |
|
470 |
379 |
321.07557 |
468 |
1265.921739 |
0.05176087601 |
19.3196112 |
|
480 |
383 |
325.63803 |
479 |
1291.713868 |
0.05524110983 |
18.10246034 |
|
490 |
384 |
330.25207 |
494 |
1299.348731 |
0.06797117791 |
14.71211815 |
|
500 |
390 |
335.00071 |
499 |
1319.096089 |
0.06497181552 |
15.39128916 |
|
510 |
391 |
339.42469 |
487 |
1330.040868 |
0.07865230332 |
12.71418582 |
|
520 |
397 |
343.69373 |
513 |
1346.045469 |
0.07311986051 |
13.67617489 |
|
530 |
400 |
348.29412 |
513 |
1350.167813 |
0.07968873983 |
12.54882436 |
|
540 |
402 |
352.51666 |
502 |
1386.876182 |
0.09196680984 |
10.87348797 |
|
550 |
406 |
356.91819 |
506 |
1380.507217 |
0.09325149258 |
10.72368894 |
|
560 |
408 |
361.02424 |
514 |
1404.888732 |
0.1050494301 |
9.519328177 |
|
570 |
411 |
365.22523 |
530 |
1422.715521 |
0.112454762 |
8.892464687 |
|
580 |
413 |
369.34287 |
521 |
1418.77839 |
0.1232202343 |
8.115550223 |
|
590 |
418 |
373.34005 |
531 |
1433.288056 |
0.1190706402 |
8.398375944 |
|
600 |
423 |
377.46866 |
553 |
1442.746338 |
0.115319667 |
8.671547757 |
|
610 |
431 |
381.44567 |
537 |
1465.369628 |
0.09774332372 |
10.23087779 |
|
620 |
436 |
385.39997 |
562 |
1472.637334 |
0.09365662155 |
10.67730165 |
|
630 |
439 |
389.13563 |
534 |
1478.156555 |
0.09732066309 |
10.27531018 |
|
640 |
442 |
393.06882 |
558 |
1481.649484 |
0.1018292447 |
9.820361553 |
|
650 |
445 |
396.90595 |
548 |
1497.393225 |
0.106959084 |
9.349369526 |
|
660 |
447 |
400.63561 |
551 |
1506.00543 |
0.1160954636 |
8.61360099 |
|
670 |
450 |
404.14945 |
559 |
1516.747995 |
0.119537528 |
8.365573694 |
|
680 |
454 |
408.04942 |
570 |
1519.082398 |
0.1192063784 |
8.388812856 |
|
690 |
455 |
411.62236 |
561 |
1527.614848 |
0.1335347632 |
7.488686663 |
|
700 |
456 |
415.03084 |
572 |
1539.163169 |
0.1481791814 |
6.748586346 |
|
710 |
460 |
418.62427 |
574 |
1539.884077 |
0.1458519987 |
6.856265318 |
|
720 |
463 |
421.97426 |
578 |
1547.427457 |
0.1484925267 |
6.73434564 |
|
730 |
464 |
425.40145 |
582 |
1555.604508 |
0.1638798245 |
6.102032409 |
|
740 |
470 |
428.68538 |
573 |
1564.879174 |
0.1481521399 |
6.749818132 |
|
750 |
476 |
431.98916 |
587 |
1570.734702 |
0.1333975079 |
7.496391917 |
|
760 |
478 |
435.42577 |
582 |
1571.44305 |
0.1414151195 |
7.071379664 |
|
770 |
481 |
438.65389 |
599 |
1584.254858 |
0.1436869055 |
6.959576424 |
|
780 |
484 |
441.67153 |
607 |
1588.947317 |
0.1441437701 |
6.937518002 |
|
790 |
489 |
445.09457 |
599 |
1600.589407 |
0.1362259478 |
7.340745404 |
|
800 |
491 |
448.31755 |
617 |
1605.023112 |
0.143349705 |
6.975947386 |
|
810 |
492 |
451.30103 |
614 |
1607.158351 |
0.1550038797 |
6.45145142 |
|
820 |
493 |
454.49558 |
615 |
1611.93494 |
0.1687692421 |
5.925250286 |
|
830 |
494 |
457.41974 |
615 |
1612.506718 |
0.1811600442 |
5.519980988 |
|
840 |
498 |
460.52534 |
616 |
1620.258478 |
0.175929077 |
5.684108715 |
|
850 |
500 |
463.43619 |
611 |
1618.179448 |
0.1816893075 |
5.503901215 |
|
860 |
502 |
466.48886 |
637 |
1626.970156 |
0.1893241908 |
5.281945196 |
|
870 |
504 |
469.32225 |
614 |
1608.774605 |
0.1936357015 |
5.164336908 |
|
880 |
506 |
472.16453 |
621 |
1626.08326 |
0.2007135869 |
4.982223751 |
|
890 |
507 |
474.83106 |
642 |
1616.914159 |
0.2118536418 |
4.720239839 |
|
900 |
508 |
477.71121 |
630 |
1630.12197 |
0.2265698161 |
4.413650579 |
|
910 |
512 |
480.52111 |
639 |
1646.293434 |
0.2189250885 |
4.567772504 |
|
920 |
515 |
483.1917 |
637 |
1646.961091 |
0.216582156 |
4.617185544 |
|
930 |
517 |
485.95266 |
643 |
1640.535159 |
0.2216791989 |
4.511023158 |
|
940 |
520 |
488.67956 |
653 |
1634.313578 |
0.2192444428 |
4.561119029 |
|
950 |
521 |
491.12097 |
651 |
1649.146596 |
0.2309380165 |
4.33016623 |
|
960 |
523 |
494.059 |
666 |
1647.011579 |
0.237884422 |
4.203722091 |
|
970 |
525 |
496.67005 |
646 |
1636.426563 |
0.2418632138 |
4.134568396 |
|
980 |
527 |
498.84554 |
649 |
1657.961282 |
0.2446417651 |
4.087609487 |
|
990 |
527 |
501.36378 |
673 |
1654.681304 |
0.2642731095 |
3.783964256 |
|
1000 |
529 |
504.20158 |
648 |
1660.686666 |
0.2714188356 |
3.684342679 |
|
1010 |
529 |
506.40903 |
657 |
1658.370444 |
0.2895342127 |
3.453823266 |
|
1020 |
532 |
508.87871 |
656 |
1638.136339 |
0.2839102453 |
3.522239921 |
|
1030 |
534 |
511.23905 |
663 |
1647.221285 |
0.2874640991 |
3.478695264 |
|
1040 |
536 |
513.77767 |
668 |
1665.580659 |
0.2930448734 |
3.412446662 |
|
1050 |
539 |
516.11837 |
662 |
1654.993519 |
0.2869025501 |
3.485504049 |
|
1060 |
541 |
518.64964 |
681 |
1670.139988 |
0.2922236238 |
3.422036818 |
|
1070 |
541 |
520.60727 |
675 |
1656.148993 |
0.3081498383 |
3.245174508 |
|
1080 |
542 |
523.04175 |
681 |
1646.860247 |
0.3201910612 |
3.123135281 |
|
1090 |
543 |
525.20885 |
681 |
1658.257932 |
0.3310934045 |
3.020295743 |
|
1100 |
543 |
527.57748 |
686 |
1656.595357 |
0.3523737641 |
2.837895729 |
Table-2: Volcanoes Random Simulation Results
|
Great Circle |
Nazca Map |
Mean |
Max |
Variance |
CDF |
Prob. of Random |
|
Width (Kms) |
Transects |
Random |
Random |
Occurrence (1/CDF) |
||
|
1 |
1 |
1.06743 |
10 |
1.103943 |
0.525585418 |
1.902640305 |
|
5 |
7 |
5.29834 |
20 |
5.974093 |
0.2431503861 |
4.11268111 |
|
10 |
16 |
10.5045 |
30 |
12.84324 |
0.06258237938 |
15.97893864 |
|
15 |
24 |
15.63637 |
40 |
20.456923 |
0.03221730367 |
31.03922073 |
|
20 |
35 |
20.69784 |
60 |
28.946339 |
0.0039267391 |
254.6642327 |
|
25 |
42 |
25.69257 |
64 |
37.619757 |
0.003921554744 |
255.0009028 |
|
26 |
44 |
26.69014 |
60 |
39.585027 |
0.002968528962 |
336.8671867 |
|
27 |
46 |
27.67653 |
65 |
41.249197 |
0.002165511682 |
461.784625 |
|
28 |
48 |
28.68181 |
63 |
43.134105 |
0.001633592009 |
612.1479503 |
|
29 |
49 |
29.66687 |
67 |
45.038554 |
0.001983468133 |
504.1674143 |
|
30 |
50 |
30.62546 |
70 |
46.54718 |
0.002257232026 |
443.0204731 |
|
31 |
50 |
31.6214 |
69 |
49.440602 |
0.004477213779 |
223.3531945 |
|
32 |
51 |
32.64077 |
76 |
50.748564 |
0.004980688373 |
200.7754602 |
|
33 |
51 |
33.55681 |
72 |
52.291873 |
0.007928833264 |
126.121961 |
|
34 |
54 |
34.50658 |
72 |
54.545397 |
0.004152364871 |
240.8266207 |
|
35 |
54 |
35.52253 |
85 |
56.756652 |
0.007090573902 |
141.0323077 |
|
40 |
60 |
40.39859 |
86 |
66.852256 |
0.008257339141 |
121.1043876 |
|
50 |
67 |
49.8339 |
103 |
87.841591 |
0.03350837487 |
29.84328556 |
|
60 |
78 |
59.10053 |
114 |
109.518224 |
0.03546284285 |
28.19852893 |
|
70 |
85 |
68.18744 |
133 |
131.316206 |
0.07116755282 |
14.05134728 |
|
80 |
98 |
77.06967 |
151 |
155.586236 |
0.0466741014 |
21.42515806 |
|
90 |
106 |
85.84118 |
161 |
179.094516 |
0.06598953331 |
15.15391835 |
|
100 |
127 |
94.42899 |
173 |
202.284058 |
0.011008378 |
90.83990394 |
|
110 |
132 |
102.91441 |
176 |
227.551104 |
0.02691889936 |
37.14862136 |
|
120 |
146 |
111.14367 |
197 |
250.558729 |
0.01383093833 |
72.30167443 |
|
130 |
152 |
119.22442 |
200 |
274.575916 |
0.02396618085 |
41.72546333 |
|
140 |
163 |
127.21034 |
219 |
298.747437 |
0.01919602778 |
52.09411091 |
|
150 |
173 |
134.95524 |
226 |
318.454017 |
0.01650659338 |
60.58185217 |
|
160 |
185 |
142.72018 |
233 |
342.060581 |
0.01112629858 |
89.87714946 |
|
170 |
192 |
150.29382 |
252 |
364.86465 |
0.01450295728 |
68.95145457 |
|
180 |
202 |
157.79507 |
250 |
390.256434 |
0.01262135224 |
79.23081304 |
|
190 |
208 |
164.99132 |
271 |
405.106165 |
0.0163055657 |
61.3287523 |
|
200 |
216 |
172.28121 |
272 |
430.787731 |
0.01758572996 |
56.86428727 |
|
210 |
222 |
179.4202 |
293 |
449.771632 |
0.02233543338 |
44.77190942 |
|
220 |
228 |
186.45187 |
290 |
468.558404 |
0.02746571029 |
36.40903474 |
|
230 |
231 |
193.27179 |
293 |
491.724 |
0.04443429082 |
22.50514145 |
|
240 |
240 |
200.00673 |
311 |
512.510905 |
0.0386485952 |
25.87416165 |
|
250 |
246 |
206.59195 |
321 |
533.380125 |
0.04397204469 |
22.74172163 |
|
260 |
253 |
213.3246 |
327 |
556.530855 |
0.0463029329 |
21.59690407 |
|
270 |
258 |
219.5861 |
338 |
567.154773 |
0.05337131114 |
18.73665793 |
|
280 |
261 |
225.94754 |
343 |
589.071208 |
0.07433796813 |
13.45207604 |
|
290 |
268 |
232.36097 |
360 |
607.981611 |
0.07417623908 |
13.48140607 |
|
300 |
275 |
238.55869 |
373 |
626.364095 |
0.07268742462 |
13.75753791 |
|
310 |
280 |
244.78349 |
364 |
643.883313 |
0.08259126895 |
12.10781736 |
|
320 |
288 |
250.63226 |
374 |
654.373027 |
0.07203822694 |
13.88151878 |
|
330 |
296 |
256.61355 |
368 |
671.534506 |
0.06426908624 |
15.55958017 |
|
340 |
306 |
262.63585 |
404 |
689.667305 |
0.04934447003 |
20.26569541 |
|
350 |
307 |
268.14099 |
405 |
706.432372 |
0.07186642608 |
13.91470335 |
|
360 |
313 |
273.76086 |
414 |
725.445872 |
0.07257790805 |
13.77829738 |
|
370 |
320 |
279.39783 |
416 |
737.042761 |
0.06738459882 |
14.8401863 |
|
380 |
331 |
284.99563 |
402 |
748.572471 |
0.04633844321 |
21.58035382 |
|
390 |
338 |
290.17282 |
413 |
755.621413 |
0.0409388648 |
24.42666656 |
|
400 |
346 |
295.77335 |
434 |
776.56512 |
0.03574317208 |
27.97737139 |
|
410 |
350 |
300.89422 |
436 |
787.912331 |
0.04010936773 |
24.93183155 |
|
420 |
358 |
306.19442 |
426 |
804.793921 |
0.03391454552 |
29.48587353 |
|
430 |
364 |
311.48155 |
442 |
817.75464 |
0.03313891359 |
30.17600433 |
|
440 |
369 |
316.43775 |
474 |
822.092725 |
0.03338525483 |
29.95334333 |
|
450 |
374 |
321.32865 |
453 |
837.253579 |
0.03435571464 |
29.10723908 |
|
460 |
379 |
326.16899 |
458 |
854.192092 |
0.03533153211 |
28.30332964 |
|
470 |
386 |
331.19889 |
451 |
862.501493 |
0.03102134521 |
32.23586835 |
|
480 |
392 |
336.05281 |
464 |
865.745641 |
0.02862205781 |
34.9380889 |
|
490 |
397 |
340.80971 |
480 |
883.4861 |
0.02934999855 |
34.07155194 |
|
500 |
401 |
345.32359 |
463 |
895.56028 |
0.03140918161 |
31.83782412 |
|
510 |
405 |
350.01436 |
475 |
901.864074 |
0.03355329088 |
29.80333594 |
|
520 |
408 |
354.59749 |
477 |
911.616776 |
0.03847151832 |
25.99325537 |
|
530 |
409 |
359.02311 |
495 |
925.706976 |
0.05023260826 |
19.90738755 |
|
540 |
412 |
363.59067 |
493 |
937.790139 |
0.05696217223 |
17.55551028 |
|
550 |
417 |
367.94185 |
493 |
932.443129 |
0.05407422593 |
18.49309875 |
|
560 |
422 |
372.06626 |
494 |
954.41211 |
0.05301306257 |
18.86327542 |
|
570 |
429 |
376.22809 |
516 |
955.073145 |
0.04385589447 |
22.80195198 |
|
580 |
431 |
380.78328 |
498 |
965.490372 |
0.05303387703 |
18.85587206 |
|
590 |
433 |
384.90707 |
514 |
971.336167 |
0.06139833737 |
16.28708598 |
|
600 |
437 |
389.01736 |
542 |
984.523759 |
0.06310449066 |
15.84673277 |
|
610 |
438 |
392.96014 |
524 |
994.257271 |
0.07658942141 |
13.05663343 |
|
620 |
444 |
397.06876 |
534 |
993.364532 |
0.06823781396 |
14.65463124 |
|
630 |
445 |
401.0429 |
545 |
1001.14926 |
0.08237875743 |
12.13905175 |
|
640 |
448 |
405.05289 |
555 |
1008.513173 |
0.08812967531 |
11.34691574 |
|
650 |
449 |
408.96138 |
538 |
1014.523228 |
0.1043701037 |
9.581287791 |
|
660 |
452 |
412.61073 |
552 |
1021.269179 |
0.1088701238 |
9.185256387 |
|
670 |
453 |
416.4361 |
559 |
1026.166817 |
0.1268486668 |
7.88340962 |
|
680 |
455 |
420.11814 |
552 |
1035.705143 |
0.1392088107 |
7.183453368 |
|
690 |
457 |
423.86861 |
554 |
1033.035347 |
0.1513130558 |
6.608815048 |
|
700 |
457 |
427.4143 |
549 |
1041.037496 |
0.1795827602 |
5.568463247 |
|
710 |
459 |
431.00524 |
576 |
1041.586033 |
0.1928561043 |
5.185213107 |
|
720 |
460 |
434.58207 |
586 |
1048.211885 |
0.2162024109 |
4.625295322 |
|
730 |
460 |
438.01121 |
567 |
1060.227344 |
0.2497006453 |
4.004795418 |
|
740 |
461 |
441.54242 |
578 |
1056.013061 |
0.274665803 |
3.640788147 |
|
750 |
464 |
444.89086 |
583 |
1060.069408 |
0.2786309267 |
3.588977046 |
|
760 |
469 |
448.38024 |
580 |
1072.115938 |
0.2644316441 |
3.781695656 |
|
770 |
470 |
451.57688 |
593 |
1070.973209 |
0.2867326527 |
3.487569311 |
|
780 |
472 |
454.92461 |
585 |
1083.679586 |
0.3019833179 |
3.311441198 |
|
790 |
476 |
458.11428 |
603 |
1080.20558 |
0.2931541947 |
3.411174113 |
|
800 |
481 |
461.20839 |
592 |
1088.029124 |
0.2742486687 |
3.646325813 |
|
810 |
482 |
464.51115 |
600 |
1085.204896 |
0.2977471264 |
3.358554664 |
|
820 |
482 |
467.64847 |
602 |
1103.311777 |
0.3328470762 |
3.004382708 |
|
830 |
484 |
471.14171 |
604 |
1082.846468 |
0.3479907504 |
2.873639598 |
Table-3: Impact Craters Random Simulation Results
|
Great Circle |
Nazca Map |
Mean |
Max |
Variance |
CDF |
Prob. of Random |
|
Width (Kms) |
Transects |
Random |
Random |
Occurrence (1/CDF) |
||
|
1 |
4 |
1.19539 |
10 |
1.258353 |
0.006206510536 |
161.1211315 |
|
4 |
10 |
4.78826 |
22 |
5.594426 |
0.01378120661 |
72.56258676 |
|
5 |
12 |
5.96336 |
27 |
7.203938 |
0.01225281205 |
81.61391816 |
|
6 |
13 |
7.16138 |
28 |
8.875296 |
0.02500773089 |
39.9876344 |
|
7 |
15 |
8.34258 |
28 |
10.640719 |
0.02063067527 |
48.47151085 |
|
8 |
17 |
9.48358 |
34 |
12.42679 |
0.01649447368 |
60.62636611 |
|
9 |
18 |
10.67208 |
35 |
14.316068 |
0.02638924255 |
37.89422899 |
|
10 |
18 |
11.84807 |
43 |
16.194667 |
0.06316806107 |
15.8307851 |
|
11 |
19 |
13.01841 |
39 |
18.264651 |
0.08081318178 |
12.37421888 |
|
12 |
19 |
14.14543 |
42 |
20.3108 |
0.1407005084 |
7.107294861 |
|
13 |
21 |
15.30301 |
52 |
22.399835 |
0.1143502186 |
8.745064173 |
|
14 |
23 |
16.4775 |
48 |
24.580874 |
0.0941584624 |
10.62039433 |
|
15 |
25 |
17.6212 |
55 |
26.830806 |
0.07714840371 |
12.96203099 |
|
16 |
25 |
18.75984 |
55 |
29.077263 |
0.1235896034 |
8.091295484 |
|
17 |
27 |
19.8972 |
55 |
31.601412 |
0.1032042078 |
9.689527403 |
|
18 |
27 |
21.01672 |
56 |
33.53 |
0.1507339324 |
6.634206274 |
|
19 |
28 |
22.15131 |
61 |
36.088755 |
0.1651320059 |
6.055761233 |
|
20 |
29 |
23.29432 |
66 |
38.465576 |
0.1787955357 |
5.592980808 |
|
30 |
40 |
34.47916 |
92 |
64.874946 |
0.2465345257 |
4.056227001 |
|
40 |
50 |
45.42652 |
105 |
94.975961 |
0.3194316886 |
3.13055979 |
|
50 |
64 |
56.00411 |
122 |
124.997573 |
0.2372485632 |
4.214988645 |
|
60 |
81 |
66.50774 |
137 |
158.66104 |
0.124961184 |
8.002484994 |
|
70 |
93 |
76.64051 |
150 |
193.054737 |
0.1195149799 |
8.367151973 |
|
80 |
102 |
86.597 |
168 |
229.731131 |
0.1547580628 |
6.461698874 |
|
90 |
114 |
96.41801 |
179 |
263.994578 |
0.1396023252 |
7.163204472 |
|
100 |
128 |
106.05148 |
187 |
301.42801 |
0.1030803582 |
9.701169234 |
|
110 |
135 |
115.43257 |
200 |
335.225333 |
0.1425971405 |
7.012763347 |
|
120 |
147 |
124.70398 |
210 |
374.207732 |
0.1245414779 |
8.029453454 |
|
130 |
153 |
133.98436 |
230 |
415.080675 |
0.1753195608 |
5.703870095 |
|
140 |
159 |
142.76677 |
242 |
445.577974 |
0.2209378456 |
4.526159822 |
|
150 |
173 |
151.48566 |
258 |
480.854414 |
0.1632672952 |
6.12492538 |
|
160 |
181 |
160.00365 |
270 |
516.597137 |
0.1778008542 |
5.624269944 |
|
170 |
192 |
168.48983 |
293 |
552.689457 |
0.158646804 |
6.303310089 |
|
180 |
200 |
176.89173 |
282 |
586.116428 |
0.1699155586 |
5.885276241 |
|
190 |
213 |
184.94776 |
303 |
617.007931 |
0.1293786169 |
7.729252517 |
|
200 |
220 |
192.9716 |
314 |
657.524893 |
0.145928341 |
6.852678468 |
|
210 |
227 |
200.71606 |
313 |
683.864958 |
0.1574265757 |
6.352167639 |
|
220 |
234 |
208.60909 |
323 |
720.008419 |
0.1720085577 |
5.813664234 |
|
230 |
238 |
216.26911 |
335 |
749.88647 |
0.2137258146 |
4.678891981 |
|
240 |
242 |
223.78594 |
342 |
779.944298 |
0.2571388815 |
3.888949015 |
|
250 |
247 |
231.14476 |
355 |
819.542105 |
0.2898429004 |
3.450144884 |
|
260 |
256 |
238.51884 |
355 |
852.434485 |
0.2746724407 |
3.640700164 |
|
270 |
258 |
245.65268 |
372 |
876.063069 |
0.3382798508 |
2.95613232 |
|
280 |
267 |
252.71854 |
383 |
902.82458 |
0.3172853487 |
3.151737085 |
|
290 |
277 |
259.64768 |
382 |
935.312711 |
0.2852257276 |
3.505995088 |
|
300 |
280 |
266.65235 |
392 |
965.351229 |
0.3337440752 |
2.996307872 |
|
310 |
284 |
273.24067 |
410 |
988.031148 |
0.3660646446 |
2.731757942 |
Table-4: Combined Sites Random Simulation Results
|
Great Circle |
Nazca Map |
Mean |
Max |
Variance |
CDF |
Prob. of Random |
|
Width (Kms) |
Transects |
Random |
Random |
Occurrence (1/CDF) |
||
|
1 |
4 |
2.55209 |
14 |
2.663547 |
0.187491181 |
5.333584196 |
|
5 |
22 |
12.6277 |
35 |
14.804793 |
0.00742905781 |
134.6065713 |
|
10 |
41 |
25.03711 |
54 |
33.171713 |
0.00278924 |
358.5206006 |
|
15 |
56 |
37.26856 |
76 |
53.666656 |
0.002327837864 |
429.5831834 |
|
20 |
80 |
49.33209 |
99 |
77.576146 |
0.000248907 |
4017.564793 |
|
25 |
98 |
61.26521 |
110 |
102.232174 |
0.000139989107 |
7143.412951 |
|
26 |
102 |
63.6099 |
129 |
108.277122 |
0.00011241 |
8896.005693 |
|
27 |
108 |
66.0185 |
118 |
113.291738 |
0.000040033557 |
24979.04446 |
|
28 |
112 |
68.37101 |
125 |
118.620962 |
0.000030897725 |
32364.8424 |
|
29 |
116 |
70.74046 |
136 |
123.8539 |
0.000023793363 |
42028.52703 |
|
30 |
119 |
73.0472 |
134 |
129.041112 |
0.000026130997 |
38268.72737 |
|
31 |
122 |
75.34145 |
142 |
135.056422 |
0.000029736803 |
33628.36281 |
|
32 |
124 |
77.70807 |
139 |
140.769927 |
0.000047766007 |
20935.39031 |
|
33 |
125 |
80.03597 |
147 |
147.275298 |
0.000105652466 |
9464.994409 |
|
34 |
132 |
82.43277 |
147 |
152.2885 |
0.000029519003 |
33876.48289 |
|
35 |
134 |
84.65352 |
149 |
158.741712 |
0.00004490089 |
22271.27346 |
|
40 |
151 |
96.17217 |
163 |
187.545587 |
0.000031196616 |
32054.75876 |
|
50 |
168 |
118.78882 |
208 |
253.347863 |
0.0000994883031 |
10051.43287 |
|
60 |
194 |
141.02102 |
224 |
321.328858 |
0.001560890533 |
640.6599174 |
|
70 |
218 |
162.66455 |
258 |
390.515923 |
0.002553801636 |
391.5730908 |
|
80 |
247 |
183.96978 |
277 |
460.188767 |
0.001650639335 |
605.8258632 |
|
90 |
277 |
204.84769 |
302 |
535.716012 |
0.000912482596 |
1095.911313 |
|
100 |
320 |
225.30833 |
345 |
612.745463 |
0.000065291942 |
15315.82565 |
|
110 |
337 |
245.36777 |
373 |
687.031795 |
0.000236226922 |
4233.217753 |
|
120 |
362 |
265.19888 |
392 |
765.948807 |
0.0002346588 |
4261.506494 |
|
130 |
382 |
284.684 |
407 |
846.266184 |
0.000411017349 |
2432.987324 |
|
140 |
404 |
303.48112 |
441 |
908.987444 |
0.000427996659 |
2336.466837 |
|
150 |
422 |
322.38346 |
459 |
999.969798 |
0.000815796023 |
1225.796611 |
|
160 |
444 |
340.70341 |
480 |
1073.878384 |
0.000810333605 |
1234.059644 |
|
170 |
462 |
358.95801 |
510 |
1161.500687 |
0.001249502463 |
800.3185505 |
|
180 |
485 |
376.70349 |
532 |
1240.469532 |
0.001053105378 |
949.5725887 |
|
190 |
500 |
394.18363 |
563 |
1314.49915 |
0.001758106438 |
568.7937763 |
|
200 |
517 |
411.18308 |
571 |
1375.696962 |
0.002165791214 |
461.7250239 |
|
210 |
530 |
428.32752 |
582 |
1454.915971 |
0.003843291343 |
260.1936493 |
|
220 |
547 |
445.16167 |
620 |
1534.805293 |
0.004668406826 |
214.2058388 |
|
230 |
557 |
461.56165 |
651 |
1615.862679 |
0.008793067804 |
113.7259512 |
|
240 |
573 |
477.6758 |
661 |
1679.261974 |
0.01000438504 |
99.95616886 |
|
250 |
587 |
493.28549 |
685 |
1754.787585 |
0.01263835912 |
79.1241957 |
|
260 |
602 |
509.14954 |
688 |
1813.388018 |
0.01461344308 |
68.43014303 |
|
270 |
615 |
525.0465 |
721 |
1897.561698 |
0.01946148546 |
51.38353914 |
|
280 |
625 |
540.12515 |
755 |
1960.099827 |
0.02761396968 |
36.21355465 |
|
290 |
649 |
554.99168 |
746 |
2032.975651 |
0.018535924 |
53.94929328 |
|
300 |
664 |
569.89871 |
770 |
2112.26969 |
0.02030520413 |
49.24845836 |
|
310 |
677 |
584.41593 |
788 |
2157.882232 |
0.02312692766 |
43.23963886 |
|
320 |
692 |
598.43504 |
784 |
2242.36338 |
0.02408426661 |
41.52088233 |
|
330 |
707 |
612.61112 |
809 |
2287.499792 |
0.02421849024 |
41.29076545 |
|
340 |
726 |
626.86294 |
832 |
2364.380555 |
0.02073435656 |
48.22913106 |
|
350 |
738 |
640.11112 |
859 |
2424.080112 |
0.02339483454 |
42.74447841 |
|
360 |
746 |
653.84835 |
862 |
2491.161772 |
0.03242436333 |
30.84100649 |
|
370 |
758 |
667.32182 |
897 |
2563.080392 |
0.03663801125 |
27.29405789 |
|
380 |
783 |
680.1201 |
898 |
2609.258756 |
0.02200172369 |
45.45098438 |
|
390 |
796 |
693.23311 |
914 |
2665.45181 |
0.02326652404 |
42.98020617 |
|
400 |
814 |
706.20757 |
929 |
2712.827345 |
0.0192469686 |
51.95623377 |
|
410 |
824 |
718.93374 |
946 |
2796.08119 |
0.02346360038 |
42.61920523 |
|
420 |
838 |
731.22764 |
933 |
2836.3268 |
0.02248983119 |
44.46454007 |
|
430 |
850 |
743.43786 |
983 |
2913.272539 |
0.02417401709 |
41.36672842 |
|
440 |
863 |
755.65347 |
983 |
2958.524327 |
0.02421586895 |
41.29523504 |
|
450 |
871 |
767.63374 |
981 |
3022.904954 |
0.03005146811 |
33.27624449 |
|
460 |
886 |
779.29083 |
1011 |
3066.210708 |
0.02698455174 |
37.05824019 |
|
470 |
900 |
791.13548 |
1046 |
3115.796805 |
0.02557008317 |
39.10820287 |
|
480 |
915 |
802.41172 |
1029 |
3187.439587 |
0.02306422332 |
43.35719379 |
|
490 |
922 |
814.07897 |
1053 |
3224.508254 |
0.02868191171 |
34.8651795 |
|
500 |
936 |
825.02025 |
1060 |
3237.188618 |
0.02555463049 |
39.13185129 |
|
510 |
942 |
836.06251 |
1071 |
3299.545842 |
0.03257248786 |
30.70075594 |
|
520 |
953 |
847.25598 |
1079 |
3351.688194 |
0.03388611634 |
29.51061107 |
|
530 |
959 |
857.94902 |
1113 |
3405.845621 |
0.04167933717 |
23.99270401 |
|
540 |
964 |
868.4549 |
1121 |
3411.768986 |
0.05094529566 |
19.62889776 |
|
550 |
973 |
878.21562 |
1133 |
3500.181428 |
0.05456598332 |
18.32643598 |
|
560 |
984 |
888.78872 |
1115 |
3555.596181 |
0.05516266352 |
18.12820368 |
|
570 |
996 |
899.44963 |
1164 |
3580.327223 |
0.05330843918 |
18.75875594 |
|
580 |
1001 |
909.35884 |
1159 |
3622.865774 |
0.06393878305 |
15.63995985 |
|
590 |
1008 |
919.07867 |
1161 |
3649.251501 |
0.07051215979 |
14.18195107 |
|
600 |
1019 |
928.8176 |
1160 |
3680.18749 |
0.06856355212 |
14.58500864 |
|
610 |
1033 |
938.79899 |
1179 |
3717.840225 |
0.06118099908 |
16.34494394 |
|
620 |
1044 |
948.45919 |
1200 |
3760.106955 |
0.05960753895 |
16.7764014 |
|
630 |
1050 |
958.09717 |
1205 |
3806.295228 |
0.06816111864 |
14.67112072 |
|
640 |
1059 |
967.08421 |
1227 |
3860.617499 |
0.06952758447 |
14.3827807 |
|
650 |
1063 |
976.46744 |
1248 |
3896.90324 |
0.08284592196 |
12.07060017 |
|
660 |
1069 |
985.56907 |
1235 |
3946.926289 |
0.09208930993 |
10.85902371 |
|
670 |
1074 |
993.96932 |
1243 |
3909.476539 |
0.1002791915 |
9.972158576 |
|
680 |
1081 |
1003.91915 |
1247 |
3953.116333 |
0.1101066603 |
9.082102725 |
|
690 |
1086 |
1011.78911 |
1294 |
4050.759835 |
0.1218067741 |
8.209724028 |
|
700 |
1088 |
1020.80695 |
1260 |
4018.741322 |
0.1445870414 |
6.916249137 |
|
710 |
1096 |
1029.14385 |
1286 |
4058.285497 |
0.1469809157 |
6.803604367 |
|
720 |
1102 |
1037.43399 |
1275 |
4106.317103 |
0.1568290951 |
6.376367851 |
|
730 |
1105 |
1046.26562 |
1325 |
4153.934986 |
0.1810680195 |
5.522786425 |
|
740 |
1114 |
1053.75957 |
1341 |
4168.303383 |
0.1753951481 |
5.701411988 |
|
750 |
1126 |
1062.66836 |
1320 |
4224.228095 |
0.1649235466 |
6.063415568 |
|
760 |
1134 |
1070.85219 |
1327 |
4220.337482 |
0.1655150159 |
6.041747901 |
|
770 |
1139 |
1078.31119 |
1354 |
4268.141571 |
0.1764592363 |
5.667031214 |
|
780 |
1145 |
1086.00084 |
1353 |
4260.138119 |
0.183016711 |
5.463981921 |
|
790 |
1156 |
1093.60453 |
1359 |
4302.748453 |
0.1707468548 |
5.856623252 |
|
800 |
1164 |
1101.58658 |
1376 |
4278.121684 |
0.1699845403 |
5.882887928 |
|
810 |
1168 |
1109.36038 |
1365 |
4330.010266 |
0.1864266254 |
5.364040666 |
|
820 |
1169 |
1116.57129 |
1375 |
4358.431398 |
0.2135532386 |
4.682673072 |
|
830 |
1174 |
1124.10626 |
1378 |
4357.648109 |
0.2248777163 |
4.446861238 |
|
840 |
1181 |
1131.73106 |
1401 |
4369.709466 |
0.2280328627 |
4.385332834 |
|
850 |
1189 |
1138.78048 |
1399 |
4431.270171 |
0.2253009996 |
4.438506717 |
|
860 |
1192 |
1145.76037 |
1420 |
4445.039207 |
0.2439828264 |
4.098649134 |
|
870 |
1196 |
1152.39085 |
1438 |
4458.018866 |
0.2568328052 |
3.893583607 |
|
880 |
1205 |
1159.75399 |
1413 |
4486.662449 |
0.249682399 |
4.005088079 |
|
890 |
1210 |
1166.87005 |
1428 |
4479.115243 |
0.2596448891 |
3.851414151 |
|
900 |
1213 |
1173.77874 |
1452 |
4531.125524 |
0.2800595931 |
3.570668618 |
|
910 |
1221 |
1180.13171 |
1443 |
4543.291422 |
0.2721514534 |
3.674424618 |
|
920 |
1227 |
1187.44829 |
1454 |
4546.858346 |
0.2787509147 |
3.587432174 |
|
930 |
1231 |
1193.42076 |
1459 |
4545.085821 |
0.2886226821 |
3.46473116 |
|
940 |
1237 |
1199.95829 |
1503 |
4570.10487 |
0.2918687194 |
3.426197922 |
|
950 |
1241 |
1206.53419 |
1470 |
4590.408551 |
0.3054807946 |
3.273528214 |
|
960 |
1245 |
1213.07763 |
1460 |
4611.649704 |
0.3191507693 |
3.133315336 |
|
970 |
1248 |
1219.44038 |
1466 |
4620.625185 |
0.3371887451 |
2.965698039 |
Table-5: ANCIENT MONUMENTS
Abydos-Oseiron— lat :26.18500, lon :31.91889, type : Monument
Abdera (Thrace)— lat :40.93333, lon :24.96667, type : Monument
Ajanta Caves— lat :20.55238, lon :75.70044, type : Monument
Aksum Obelisk— lat :14.13217, lon :38.71967, type : Monument
Amaru Muru— lat :-16.1708, lon :-69.5412, type : Monument
Ancyra— lat :39.93333, lon :32.86667, type : Monument
Angkor Thom— lat :13.43950, lon :103.86220, type : Monument-Satellite—ANGKOR
ANGKOR WAT— lat :13.4125, lon :103.8667, type : Monument—CAPITAL
Anundshog Tumulus— lat :59.63056, lon :16.64472, type : Monument
Arkaim— lat :52.62694, lon :59.56111, type : Monument
Asuka Megaliths— lat :34.03333, lon :135.81667, type : Monument
Avebury— lat :51.42861, lon :-1.85417, type : Monument-Satellite-SILSBURY
Aztalan Mound— lat :43.06455, lon :-88.86223, type : Monument
Aztec Ruins— lat :36.83584, lon :-107.99812, type : Monument
BaalBek— lat :34.00634, lon :36.20732, type : Monument
BadaValley Megaliths— lat :-1.8800, lon :120.2200, type : Monument
BALLYCROVANE Stone— lat :51.71287, lon :-9.94458, type : Monument—CAPITAL
BALNUARAN of CLAVA— lat :57.4737, lon :-4.0744, type : Monument—HIGHLANDS—CAPITAL
BARNENEZ— lat :48.66750, lon :-3.85861, type : Monument—BARNENEZ—CAPITAL
Barpa Langass— lat :57.57056, lon :-7.29167, type : Monument
BELTRANA Temple— lat :39.97875, lon :3.98008, type : Monument—MINORCA—CAPITAL
Borobudur— lat :-7.60787, lon :110.20373, type : Monument
Borrehaugene— lat :59.38250, lon :10.45944, type : Monument
Boswens Menhir— lat :50.13904, lon :-5.63989, type : Monument
Brihadeeswara Temple— lat :10.78278, lon :79.13167, type : Monument
Brownshill Dolmen— lat :52.8375, lon :-6.8811, type : Monument
BRYNCELLIDDU— lat :53.2077, lon :-4.2361, type : Monument—BRYN—CAPITAL
Bryn Cader Faner Circle— lat :52.8982, lon :-4.0114, type : Monument-Satellite—BRYN
Caddoan Mounds— lat :31.59532, lon :-95.14981, type : Monument
Cahuachi— lat :-14.81861, lon :-75.11667, type : Monument-Satellite—NAZCA
CallanishStones— lat :58.1979, lon :-6.7443, type : Monument
Caral— lat :-10.89361, lon :-77.52028, type : Monument
CARNAC— lat :47.58470, lon :-3.07341, type : Monument—CAPITAL
Carthage— lat :36.85280, lon :10.32330, type : Monument
Casa Grande— lat :32.99701, lon :-111.53207, type : Monument
Catalhoyuk— lat :37.66667, lon :32.82806, type : Monument
Cempoala— lat :19.44500, lon :-96.40889, type : Monument
Chetroketl— lat :36.0600, lon :-107.9500, type : Monument
Chan Chan— lat :-8.10583, lon :-79.07444, type : Monument-Satellite—ELBRUJO
Corrimony Cairn— lat :57.33484, lon :-4.68949, type : Monument-Satellite—HIGHLANDS
Costa Rica Stone Spheres— lat :8.91139, lon :-83.47750, type : Monument
Crantit Cairn— lat :58.97138, lon :-2.95452, type : Monument-Satellite—ORKNEY
Cuween Hill— lat :58.99712, lon :-3.10778, type : Monument-Satellite—ORKNEY
Derinkuyu— lat :38.36667, lon :34.73333, type : Monument
Dhamek Stupa-Varanasi— lat :25.3808, lon :83.0245, type : Monument
Dholavira— lat :23.88611, lon :70.21667, type : Monument
Dilmun— lat :26.19667, lon :50.48556, type : Monument
Dogon-Tellem Caves (Sangha)— lat :14.3588, lon :-3.5950, type : Monument
Dowth— lat :53.70365, lon :-6.4502, type : Monument-Satellite—NEWGRANGE
Dolmen De Menga— lat :37.02459, lon :-4.54629, type : Monument
Dulan Ruins— lat :22.88494, lon :121.21978, type : Monument
Dwarkadhish Temple— lat :22.23789, lon :68.96756, type : Monument
Dzibilchaltun— lat :21.09100, lon :-89.59030, type : Monument-Satellite—ACANCEH
Effigy Mounds— lat :43.09413, lon :-91.18208, type : Monument
ELBRUJO— lat :-7.91498, lon :-79.30549, type : Monument—CAPITAL
Elephanta Caves— lat :18.96325, lon :72.93144, type : Monument
Emerald Mound— lat :38.63056, lon :-89.78583, type : Monument
Er Lannic— lat :47.56806, lon :-2.89694, type : Monument-Satellite—CARNAC
Etowah Mounds— lat :34.12515, lon :-84.80764, type : Monument
Frostatinget Bautasten— lat :63.56750, lon :10.70222, type : Monument
GALLARDET tomb— lat :43.58650, lon :3.51010, type : Monument—CAPITAL
Ganeriwala— lat :28.50000, lon :71.06667, type : Monument
Gavrinis— lat :47.5740, lon :-2.8970, type : Monument-Satellite—CARNAC
Gila Cliff Dwellings— lat :33.22722, lon :-108.27222, type : Monument
Gobekli Tepe— lat :37.22306, lon :38.92250, type : Monument
GGANTIJA— lat :36.04722, lon :14.26917, type : Monument—MALTA—CAPITAL
Gochang Dolmens— lat :34.96667, lon :126.92917, type : Monument
Golden Temple-Amritsar— lat :31.62000, lon :74.87694, type : Monument
Gonur Tepe— lat :38.2140, lon :62.0379, type : Monument
Grande Menhir Brise— lat :47.57165, lon :-2.94959, type : Monument-Satellite—CARNAC
Grande Menhir Counozouls— lat :42.72960, lon :2.22390, type : Monument
Grand Mound-Minnesota— lat :48.51667, lon :-93.70861, type : Monument
Grave Creek Mound— lat :39.91691, lon :-80.74458, type : Monument
GREAT PYRAMID of GIZA— lat :29.97918, lon :31.13436, type : Monument—CAPITAL
Great Zimbabwe— lat :-20.29667, lon :30.93333, type : Monument
Great Stupa-Amravati— lat :16.57300, lon :80.35800, type : Monument-Satellite—UNDAVALLI
Grey Cairns of Camster— lat :58.3791, lon :-3.2642, type : Monument
Gunung Padang Megaliths— lat :-6.99347, lon :107.05638, type : Monument
Harappa— lat :30.62889, lon :72.86389, type : Monument
Hattusa— lat :40.01972, lon :34.61528, type : Monument
Heliopolis-Obelisk— lat :30.12933, lon :31.30753, type : Monument-Satellite—GIZA
Hill of Tara— lat :53.57750, lon :-6.61194, type : Monument-Satellite—NEWGRANGE
Holm of Papa— lat :59.35053, lon :-2.86868, type : Monument-Satellite—ORKNEY
Hulbjerg Jaettestue— lat :54.73612, lon :10.68419, type : Monument
Isbister Cairn— lat :58.7391, lon :-2.9314, type : Monument-Satellite—ORKNEY
Jelling Stones— lat :55.75583, lon :9.41944, type : Monument
Jetavanaramaya Stupa— lat :8.35167, lon :80.40361, type : Monument
Jokhang Temple-Lhasa— lat :29.65306, lon :91.04750, type : Monument
Kaimanawa Wall-Lk.Taupo— lat :-38.94921, lon :176.18670, type : Monument
Khajuraho-Vamana Temple— lat :24.35306, lon :79.91944, type : Monument
Kings Grave-Sweden— lat :55.68333, lon :14.23333, type : Monument
Knap of Howar— lat :59.34931, lon :-2.91089, type : Monument-Satellite—ORKNEY
Knossos— lat :35.29806, lon :25.16306, type : Monument
Knowe of Yarso— lat :59.13912, lon :-3.04158, type : Monument-Satellite—ORKNEY
Knowth— lat :53.70167, lon :-6.49167, type : Monument-Satellite—NEWGRANGE
Komakino StoneCircle— lat :40.73856, lon :140.72863, type : Monument
Kuelap— lat :-6.41861, lon :-77.92333, type : Monument
Kukui Heiau— lat :21.05972, lon :-156.84306, type : Monument
Kyaiktiyo Pagoda-Rock— lat :17.48168, lon :97.09812, type : Monument
La Draille— lat :43.75510, lon :3.70660, type : Monument
La Hougue Bie— lat :49.2006, lon :-2.0638, type : Monument-Satellite—CARNAC
Lei Cheng Uk Han-HongKong— lat :22.33809, lon :114.16002, type : Monument
Lake Jackson Mounds— lat :30.50089, lon :-84.31164, type : Monument
Leluh Ruins-Kosrae— lat :5.33333, lon :163.03333, type : Monument
Listoghil— lat :54.25050, lon :-8.51820, type : Monument
Lubaantum— lat :16.28111, lon :-88.96500, type : Monument
Machaquila— lat :15.76667, lon :-89.38333, type : Monument
Machu Picchu— lat :-13.16333, lon :-72.54556, type : Monument-Satellite-SACSAYHUAMAN
MAESHOWE— lat :58.9966, lon :-3.1882, type : Monument—ORKNEY—CAPITAL
Maykop Kurgan— lat :44.35153, lon :40.41028, type : Monument
Menhirs CHAM de BONDONS— lat :44.4, lon :3.6, type : Monument—CAPITAL
Menhir DuBac— lat :44.39615, lon :3.41380, type : Monument-Satellite—BONDONS
Menhir De Champ Dolent— lat :48.53500, lon :-1.73917, type : Monument
Menhir De La Leque— lat :44.19293, lon :4.39452, type : Monument
Menhir De MALVES— lat :43.25327, lon :2.43564, type : Monument—CAPITAL
Menhir De Picarel— lat :43.3742, lon :2.1616, type : Monument-Satellite—MALVES
Menhir Du Pla Del Bac— lat :42.47725, lon :2.07092, type : Monument
Menhir DuRun— lat :48.77934, lon :-3.33495, type : Monument-Satellite—BARNENEZ
Menhir Glomel— lat :48.58150, lon :-3.34410, type : Monument-Satellite—KAILOUAN
Menhir Kailouan— lat :48.44833, lon :-3.12056, type : Monument—CAPITAL
Menhir Kerien— lat :48.39302, lon :-3.21454, type : Monument-Satellite—KAILOUAN
Menhirs Kergadiou— lat :48.49358, lon :-4.72499, type : Monument-Satellite—KERLOAS
Menhir KERLOAS— lat :48.42667, lon :-4.67928, type : Monument——CAPITAL
Menhirs Le Coulet— lat :43.80983, lon :3.51889, type : Monument-Satellite—GALLARDET
Menhir Louargat— lat :48.58150, lon :-3.34410, type : Monument-Satellite—BARNENEZ
Menhir Men Marz— lat :48.67030, lon :-4.3352, type : Monument-Satellite—BARNENEZ
Menhir Pedernec— lat :48.61, lon :-3.30028, type : Monument-Satellite—BARNENEZ
Menhir Pedra Dreta De Llivia— lat :42.45889, lon :1.97034, type : Monument
Menhir Pyrolles— lat :42.95083, lon :2.34056, type : Monument-Satellite—MALVES
Merrivale Stone— lat :50.55306, lon :-4.04306, type : Monument
MesaVerde-SunTemple— lat :37.16458, lon :-108.47532, type : Monument
Mohenjo-Daro— lat :27.32917, lon :68.13889, type : Monument
Monks Mound-Cahokia— lat :36.66057, lon :-90.06211, type : Monument
Monte Alban— lat :17.04389, lon :-96.76778, type : Monument
Moundville Mounds, lat :33.00788, lon :-87.63134, type : Monument
Midhowe Cairn— lat :59.15660, lon :-3.09920, type : Monument-Satellite—ORKNEY
Murujuga— lat :-20.5583, lon :116.8333, type : Monument
NAZCA-spider— lat :-14.69434, lon :-75.12270, type : Monument—GEOGLYPH—CAPITAL
Nabta Playa— lat :22.5333, lon :30.7000, type : Monument
NanMadol Ruins-Ponhpei— lat :6.84194, lon :158.33222, type : Monument
Naveta D’es Tudons— lat :40.00313, lon :3.89156, type : Monument-Satellite—MINORCA
Necropolis Cerveteri— lat :42.0000, lon :12.1000, type : Monument
NEWGRANGE— lat :53.69437, lon :-6.47503, type : Monument——CAPITAL
Ocmulgee Mounds— lat :32.83684, lon :-83.60834, type : Monument
Ollantaytambo— lat :-13.25806, lon :-72.26333, type : Monument-Satellite-SACSAYHUAMAN
Oshoro Stone Circle— lat :43.19943, lon :140.87471, type : Monument
Oyu Stone Circle— lat :40.27167, lon :140.80389, type : Monument
Pachacamac— lat :-12.25667, lon :-76.90028, type : Monument
Palenque— lat :17.48398, lon :-92.04633, type : Monument
Paquime— lat :30.36630, lon :-107.94743, type : Monument
Persepolis— lat :29.93444, lon :52.89139, type : Monument
Petra— lat :30.32861, lon :35.44194, type : Monument
Phimai— lat :15.22083, lon :102.49389, type : Monument
Poverty Point Bird Mound— lat :32.63525, lon :-91.41121, type : Monument
Prasat Ta Muen Thom— lat :14.34917, lon :103.26639, type : Monument-Satellite—ANGKOR
Preah Ko— lat :13.34389, lon :103.97278, type : Monument-Satellite—ANGKOR
Preah Vihear— lat :14.39306, lon :104.68028, type : Monument
Pylos-Palace of Nestor— lat :37.02705, lon :21.69484, type : Monument
Pyramid ACANCEH— lat :20.8167, lon :-89.4500, type : Monument—CAPITAL
Pyramid AltunHa— lat :17.76395, lon :-88.34706, type : Monument
Pyramid (Bent & Red)— lat :29.79028, lon :31.20917, type : Monument-Satellite—GIZA
Pyramid BONAMPAK— lat :16.70400, lon :-91.06500, type : Monument—CAPITAL
Pyramid CALAKMUL— lat :18.10539, lon :-89.81083, type : Monument—CAPITAL
Pyramid Chichen-Itza— lat :20.68278, lon :-88.56861, type : Monument
Pyramid Cholula— lat :19.05750, lon :-98.30194, type : Monument
Pyramid COBA— lat :20.49472, lon :-87.73611, type : Monument—CAPITAL
Pyramid Cuicuilco— lat :19.30167, lon :-99.18167, type : Monument-Satellite—TEOTIHUACAN
Pyramid Djoser— lat :29.87127, lon :31.21639, type : Monument-Satellite—GIZA
Pyramid ElMirador— lat :17.75505, lon :-89.92043, type : Monument-Satellite—CALAKMUL
Pyramid Guachimontones— lat :20.69491, lon :-103.83609, type : Monument
Pyramid LaVenta— lat :18.10330, lon :-94.04019, type : Monument
Pyramid Meidum— lat :29.38806, lon :31.15694, type : Monument-Satellite—GIZA
Pyramid PiedrasNegras— lat :17.16667, lon :-91.26250, type : Monument-Satellite—BONAMPAK
Pyramid Quirigua— lat :15.26944, lon :-89.04028, type : Monument
Pyramid Tenayuca— lat :19.53217, lon :-99.16847, type : Monument-Satellite—TEOTIHUACAN
Pyramid Teotenango— lat :19.10861, lon :-99.59722, type : Monument
Pyramid TIKAL— lat :17.22194, lon :-89.62278, type : Monument—CAPITAL
Pyramid Tres Zapotes— lat :18.46782, lon :-95.43750, type : Monument
Pyrmid Uaxactun— lat :17.39356, lon :-89.63453, type : Monument-Satellite—TIKAL
Pyramid Uxmal— lat :20.35944, lon :-89.77139, type : Monument
Pyramid Xian (Emperor’s Tomb)— lat :34.38124, lon :109.25401, type : Monument
Quanterness Cairn— lat :59.01667, lon :-3.01667, type : Monument-Satellite—ORKNEY
Quoyness Cairn— lat :59.22555, lon :-2.56824, type : Monument-Satellite—ORKNEY
Rapa Nui-Orongo— lat :-27.18944, lon :-109.44250, type : Monument
Ring of Brodgar— lat :59.00200, lon :-3.22870, type : Monument-Satellite—ORKNEY
Rhuba An Dunain— lat :56.68168, lon :-5.68319, type : Monument
Rollright Stones— lat :51.97553, lon :-1.57081, type : Monument
Saint Paul Mound— lat :44.94571, lon :-93.05650, type : Monument
SACSAYHUAMAN— lat :-13.50778, lon :-71.98222, type : Monument—CAPITAL
Sanchi Stupa— lat :23.48066, lon :77.73630, type : Monument
San Lorenzo Tenochtitlan— lat :17.75361, lon :-94.76000, type : Monument
Sechin Bajo— lat :-9.46472, lon :-78.26500, type : Monument
SerpentMound— lat :39.02520, lon :-83.43020, type : Monument
Shahr-eSukhteh— lat :30.59528, lon :61.32639, type : Monument
SHANBALLYEDMOND Court— lat :52.68020, lon :-8.23364, type : Monument
SILSBURY HILL— lat :51.41556, lon :-1.85750, type : Monument—CAPITAL
Skara Brae— lat :59.04861, lon :-3.34306, type : Monument-Satellite—ORKNEY
Snoldelev Stone— lat :55.57167, lon :12.12139, type : Monument
Stonehenge— lat :51.17884, lon :-1.82619, type : Monument-Satellite-SILSBURY
Stonehenge of America— lat :42.84196, lon :-71.20969, type : Monument
Stora Hammars Stones— lat :57.85297, lon :19.02867, type : Monument
Tanis— lat :30.97694, lon :31.88000, type : Monument-Satellite—GIZA
Tarxien Temples— lat :35.86917, lon :14.51194, type : Monument-Satellite—MALTA
Taversoe Tuick— lat :59.13200, lon :-2.98800, type : Monument-Satellite—ORKNEY
Tell Qaramel— lat :36.378, lon :37.275, type : Monument
Temple of Hera-Paestum— lat :40.42222, lon :15.00528, type : Monument
TEOTIHUACAN-Sun-Pyramid— lat :19.69240, lon :-98.84361, type : Monument—CAPITAL
TIWANAKU-Akapana Pyramid— lat :-16.55472, lon :-68.67333, type : Monument—CAPITAL
Toltec Mounds— lat :34.64694, lon :-92.06528, type : Monument
Toolsboro Mounds— lat :41.1428, lon :-91.0629, type : Monument
Treasury of Atreus— lat :37.7268, lon :22.7539, type : Monument
Troy— lat :39.95750, lon :26.23889, type : Monument
Tulum— lat :20.21472, lon :-87.42889, type : Monument-Satellite—COBA
Tumulus of Bougon— lat :46.3740, lon :-0.0675, type : Monument
Tumulus of St.Michael— lat :47.58779, lon :-3.07341, type : Monument-Satellite—CARNAC
Tyre— lat :33.27083, lon :35.19611, type : Monument
UNDAVALLI Caves— lat :16.49570, lon :80.58000, type : Monument—CAPITAL
Unstan Cairn— lat :58.9863, lon :-3.2492, type : Monument-Satellite—ORKNEY
Vaishali-Asokan Pillar— lat :25.9900, lon :85.1300, type : Monument
Van Fortress— lat :38.50321, lon :43.33913, type : Monument
Vasterljung Runestone— lat :58.91667, lon :17.43333, type : Monument
Vera Island Megaliths— lat :55.16145, lon :60.03112, type : Monument
Vinquoy Cairn— lat :59.22712, lon :-2.77250, type : Monument-Satellite—ORKNEY
Waylands Smithy— lat :51.56723, lon :-1.59526, type : Monument-Satellite-SILSBURY
West Kennet Long Barrow— lat :51.40856, lon :-3.04158, type : Monument
Yakushima Megaliths– lat :30.3552, lon :130.5238, type : Monument
Yaxchilan— lat :16.90000, lon :-90.96667, type : Monument-Satellite—BONAMPAK
Yin Xu (Ruins of Yin-Anyang)— lat :36.13944, lon :114.30306, type : Monument
Ziggurat Dur Kurigalzu— lat :33.35361, lon :44.20222, type : Monument
Ziggurat-UR— lat :30.96278, lon :46.10306, type : Monument
Ziggurat Chogha Zanbil— lat :32.00833, lon :48.52083, type : Monument
Zorats Karer-Karahunj— lat :39.5507, lon :46.0286, type : Monument ]}
GEOGLYPH-Blythe— lat :33.80049, lon :-114.53197, type : GEOGLYPH
GEOGLYPH-Candelabra-Paracas— lat :-13.79458, lon :-76.30870, type : GEOGLPYH
GEOGLYPH-CerneAbbas— lat :50.81361, lon :-2.47472, type : GEOGLYPH-Satellite-SILSBURY
SUBMERGED-Guanahacabibes— lat :21.87889, lon :-84.82306, type : SUBMERGED
SUBMERGED-Gulf of Cambay— lat :21.8891, lon :72.3784, type : SUBMERGED
SUBMERGED-Kerama Stone Circle— lat :26.19900, lon :127.28056, type : SUBMERGED
SUBMERGED-Yonaguni— lat :24.4320, lon :123.0110, type : SUBMERGED
Ithaka— lat :38.36667, lon :20.71667, type : OTHER
Marcahuasi— lat :-11.78889, lon :-76.57361, type : OTHER
Nord— lat :81.71667, lon :-17.79917, type : OTHER
Nuuk— lat :64.17500, lon :-51.73889, type : OTHER
Olympus— lat :40.08556, lon :22.35861, type : OTHER
Pitoravik— lat :77.96667, lon :-72.21667, type : OTHER
Ramanadessa-Hanthawaddy— lat :17.33667, lon :96.47972, type : OTHER
Sigiriya Elephant Rock— lat :7.95694, lon :80.75972, type : OTHER
Sukhothai— lat :17.02111, lon :99.70361, type : OTHER
Uluru— lat :-25.34500, lon :131.03611, type : OTHER
Table-6: VOLCANOES
Pico_de_Orizaba — lat :19.0303, lon :-97.2681, type : Volcano -N_America -ULTRA // 5636/4922 strato
Popocatepetl — lat :19.022, lon :-98.628, type : Volcano -N_America -ULTRA // 5426m
Iztaccihatl — lat :19.1789, lon :-98.6417, type : Volcano -N_America -ULTRA // 5230m
Mt.Bona — lat :61.3856, lon :-141.7486, type : Volcano -N_America -ULTRA // 5005m
Mt.Blackburn — lat :61.7317, lon :-143.4331, type : Volcano -N_America -ULTRA // 4996m
Mt.Sanford — lat :62.2139, lon :-144.1289, type : Volcano -N_America -ULTRA // 4949m
Mt.Churchill — lat :61.4194, lon :-141.7147, type : Volcano -N_America // 4766/362 stat-cal
Nevado_de_Toluca — lat :19.1017, lon :-99.7675, type : Volcano -N_America -ULTRA // 4680/2210 strato
Sierra_Negra — lat :18.983, lon :-97.317, type : Volcano -N_America // 4580m
La_Malinche — lat :19.2308, lon :-98.0319, type : Volcano -N_America -ULTRA // 4461m
Mt.Rainier — lat :46.8529, lon :-121.7604, type : Volcano -N_America -ULTRA -DECADE // 4392m
Nevado_de_Colima — lat :19.5124, lon :-103.6170, type : Volcano -N_America -DECADE // 4340/600 strato
Mt.Shasta — lat :41.4092, lon :-122.1949, type : Volcano -N_America -ULTRA // 4322m strato
Mt.Wrangell — lat :62.00572, lon :-144.01935, type : Volcano -N_America -ULTRA // 4317m shield
Cofre_de_Perote — lat :19.492, lon :-97.150, type : Volcano -N_America // 4282m
Atna_Peaks — lat :61.7494, lon :-143.2397, type : Volcano -N_America -ULTRA // 4220m
Damavand — lat :35.9548, lon :52.1100, type : Volcano -Asia -ULTRA // 5610m strato
Ararat — lat :39.7019, lon :44.2983, type : Volcano -Asia -ULTRA // 5165m complex
Sabalan — lat :38.2669, lon :47.8369, type : Volcano -Asia -ULTRA // 4811m
Klyuchevskaya_Sopka — lat :56.0575, lon :160.6415, type : Volcano -Asia -ULTRA // 4750/4649 strato
Kamen — lat :56.020, lon :160.593, type : Volcano -Asia -ULTRA // 4579m
Krestovsky — lat :56.11328, lon :160.50719, type : Volcano -Asia // 4108m
Aragats — lat :40.533, lon :44.20, type : Volcano -Asia -ULTRA // 4090m strato
Suphan_Dagi — lat :38.9317, lon :42.8342, type : Volcano -Asia -ULTRA // 4058m
Taftan — lat :28.6000, lon :61.1325, type : Volcano -Asia -ULTRA // 4042m-3981m
Ushkovsky — lat :56.070, lon :160.470, type : Volcano -Asia // 3943m
Little_Ararat — lat :39.6475, lon :44.4125, type : Volcano -Asia // 3925/1200 strato
Erciyes_Dagi — lat :38.5318, lon :35.4470, type : Volcano -Asia -ULTRA // 3916m
Mt.Kerinci — lat :-1.6967, lon :101.2642, type : Volcano -Asia -ULTRA // 3805m strato
Mt.Fuji — lat :35,3581, lon :138.7311, type : Volcano -Asia -ULTRA // 3776m strato
Rinjani — lat :-8.4144, lon :116.4598, type : Volcano -Asia -ULTRA // 3726m
Sahand — lat :37.7308, lon :46.5000, type : Volcano -Asia -ULTRA // 3707m
Elbrus — lat :43.3499, lon :42.4453, type : Volcano -Europe -ULTRA // 5642m strato
Kazbek — lat :42.6992, lon :44.5183, type : Volcano -Europe -ULTRA // 5047m
Mt.Etna — lat :37.7510, lon :14.9934, type : Volcano -Europe -ULTRA -DECADE // 3329m strato
Mt.Pico — lat :38.4687, lon :-28.3993, type : Volcano -Europe -ULTRA // 2351m strato
Beerenberg — lat :71.0833, lon :-8.1667, type : Volcano -Europe -ULTRA // 2277m strato
Oraefajokull — lat :64.0217, lon :-16.6433, type : Volcano -Europe -ULTRA // 2109m strato
Bardarbunga — lat :64.6410, lon :-17.5280, type : Volcano -Europe // 2009m
Kverkfjoll — lat :64.650, lon :-16.717, type : Volcano -Europe // 1920m
Puy_de_Sancy — lat :45.5283, lon :2.8142, type : Volcano -Europe -ULTRA // 1885m strato
Puy_Mary — lat :45.109, lon :2.676, type : Volcano -Europe // 1783m
Snaefell — lat :64.8057, lon :-23.7731, type : Volcano -Europe // 1446m
Hofsjokull — lat :64.817, lon :-18.817, type : Volcano -Europe // 1782m
Esjufjoll — lat :64.27, lon :-16.65, type : Volcano -Europe // 1760m strato
Grimsvotn — lat :64.42, lon :-16.33, type : Volcano -Europe // 1725m
Herdubreid — lat :65.1789, lon :-16.3473, type : Volcano -Europe // 1682m
Eiriksjokull — lat :64.7697, lon :-20.4020, type : Volcano -Europe // 1675m
Mt.Kilimanjaro — lat :-3.0758, lon :37.3533, type : Volcano -Africa -ULTRA // 5895m strato
Mt.Kenya — lat :-.1508, lon :37.3075, type : Volcano -Africa -ULTRA // 5199m
Mt.Meru — lat :-3.247, lon :36.748, type : Volcano -Africa -ULTRA // 4568m strato
Mt.Karisimbi — lat :-1.508, lon :29.445, type : Volcano -Africa -ULTRA // 4507m
Mt.Mikeno — lat :-1.464, lon :29.418, type : Volcano -Africa // 4437/1190 strato
Mt.Elgon — lat :1.118, lon :34.525, type : Volcano -Africa -ULTRA // 4321m shield
Mt.Muhavura — lat :-1.3806, lon :29.6773, type : Volcano -Africa -ULTRA // 4127m
Mt.Cameroon — lat :4.217, lon :9.173, type : Volcano -Africa -ULTRA // 4040m strato
Pico_de_Teide — lat :28.273, lon :-16.639, type : Volcano -Africa -ULTRA -DECADE // 3718/3718 str/shield
Mt.Bisoke — lat :-1.461, lon :29.482, type : Volcano -Africa // 3711m
Mt.Sabyinyo — lat :-1.4, lon :29.6, type : Volcano -Africa // 3645m
Mt.Gahinga — lat :-1.3873, lon :29.6435, type : Volcano -Africa -ULTRA // 3474m
Mt.Nyiragongo — lat :-1.5220, lon :29.2495, type : Volcano -Africa -DECADE // 3470m strato
Mt.Hanang — lat :-4.435, lon :35.4, type : Volcano -Africa -ULTRA // 3420m
Emi_Koussi — lat :19.7936, lon :18.5519, type : Volcano -Africa -ULTRA // 3445m shield
Mt.Giluwe — lat :-6.043, lon :143.887, type : Volcano -Oceania -ULTRA // 4367m shield
Mauna_Kea — lat :19.8207, lon :-155.4681, type : Volcano -Oceania -ULTRA // 4207m shield
Mauna_Loa — lat :19.4795, lon :-155.6027, type : Volcano -Oceania -ULTRA -DECADE // 4169m shield
Mt.Hagen — lat :-5.8582, lon :-144.2429, type : Volcano -Oceania // 3778m
Doma_Peaks — lat :-5.90, lon :143.15, type : Volcano -Oceania // 3568m
Mt.Kerewa — lat :-6.0681, lon :-143.1365, type : Volcano -Oceania // 3340m
Mt.Yelia — lat :-7.05, lon :145.858, type : Volcano -Oceania // 3384m
Crater_Mountain — lat :-6.58, lon :145.08, type : Volcano -Oceania // 3233m
Haleakala — lat :20.7097, lon :-156.2533, type : Volcano -Oceania -ULTRA // 3055m shield
Ruapehu — lat :-39.2817, lon :175.5685, type : Volcano -Oceania -ULTRA // 2797m strato
Mt.Balbi — lat :-5.917, lon :-154.983, type : Volcano -Oceania -ULTRA // 2715m
Mt.Suaru — lat :-6.25, lon :144.83, type : Volcano -Oceania // 2667m
Mt.Sisa — lat :-10.65, lon :152.817, type : Volcano -Oceania // 2650m
Mt.Kirimwi — lat :-6.5652, lon :144.7659, type : Volcano -Oceania // 2566m
Mt.Sidley — lat :-77.03, lon :-126.1, type : Volcano -Antarctica -ULTRA // 4285m shield
Mt.Erebus — lat :-77.5297, lon :167.1533, type : Volcano -Antarctica -ULTRA // 3794m COMPLEX
Mt.Frakes — lat :-76.8, lon :-117.7, type : Volcano -Antarctica -ULTRA // 3675m shield
Toney_Mountain — lat :-75.8, lon :-115.817, type : Volcano -Antarctica -ULTRA // 3595m shield
Mt.Steere — lat :-76.7, lon :-117.8, type : Volcano -Antarctica // 3558m shield
Mt.Berlin — lat :-76.05, lon :-135.87, type : Volcano -Antarctica -ULTRA // 3478m shield
Mt.Takahe — lat :-77.217, lon :166.800, type : Volcano -Antarctica -ULTRA // 3460m shield
Mt.Overlord — lat :-73.17, lon :164.6, type : Volcano -Antarctica // 3395m strato
Mt.Waesche — lat :-77.17, lon :-126.9, type : Volcano -Antarctica // 3392m ?
Mt.Hampton — lat :-76.483, lon :-125.8, type : Volcano -Antarctica // 3323m shield
Mt.Terror — lat :-77.52, lon :168.53, type : Volcano -Antarctica -ULTRA // 3230m shield
Mt.Siple — lat :-73.43, lon :-126.66, type : Volcano -Antarctica -ULTRA // 3110/3110 shield
Mt.Moulton — lat :-76.05, lon :-135.13, type : Volcano -Antarctica // 3078m shield
Ojos_del_Salado — lat :-27.1097, lon :-68.5414, type : Volcano -S_America -ULTRA // 6887m strato
Monte_Pissis — lat :-27.7558, lon :-68.7992, type : Volcano -S_America -ULTRA // 6882m
Cerro_Bonete — lat :-28.0186, lon :-68.756, type : Volcano -S_America // 6759m
Nevado_Tres_Cruces — lat :-27.1, lon :-68.783, type : Volcano -S_America // 6749m
Lluillaillaco — lat :-24.7207, lon :-68.5366, type : Volcano -S_America -ULTRA // 6723m
Cerro_Cazadero — lat :-27.1945, lon :-68.5609, type : Volcano -S_America // 6658m
Nevado_Incahuasi — lat :-27.0333, lon :-68.2958, type : Volcano -S_America -ULTRA // 6621m
Cerro_Tupungato — lat :-33.358, lon :-69.770, type : Volcano -S_America -ULTRA // 6550m
Nevado_Sajama — lat :-18.1050, lon :-68.8794, type : Volcano -S_America -ULTRA // 6542m
Nevado_El_Muerto — lat :-27.067, lon :-68.483, type : Volcano -S_America // 6488m
Cerro_Veladero — lat :-28.517, lon :-68.983, type : Volcano -S_America // 6436m
Cerro_Nacimiento — lat :-27.2806, lon :-68.5125, type : Volcano -S_America -ULTRA // 6436m
Nevado_Coropuna — lat :-15.4731, lon :-72.0750, type : Volcano -S_America -ULTRA // 6428m
Volcan_Antofalla — lat :-25.5625, lon :-67.8808, type : Volcano -S_America -ULTRA // 6409m
Nevado_de_Cachi — lat :-24.9317, lon :-66.3908, type : Volcano -S_America // 6380m
Cerro_El_Condor — lat :-26.6317, lon :-68.3617, type : Volcano -S_America -ULTRA // 6373/1660 strato
Mt.Drum — lat :62.1161, lon :-144.6378, type : Volcano -ULTRA // 3660/2050 strato
Shishaldin — lat :54.7554, lon :-163.9709., type : Volcano -ULTRA // 2869/2869 strato
Mt.Baker — lat :48.7767, lon :-121.8144, type : Volcano -ULTRA // 3286/2686 strato
Mt.Adams — lat :46.2024, lon :-121.4910, type : Volcano -ULTRA // 3743/2474 strato
Mt.St.Helens — lat :46.1914, lon :-122.1956, type : Volcano -ULTRA -VEI // 2549/1404:1804 strato
Mt.Hood — lat :45.3736, lon :-121.6960, type : Volcano -ULTRA // 3429/2349 strato
Lassen_Peak — lat :40.4882, lon :-121.5049, type : Volcano -ULTRA // 3187/1594 LavaDome
Glacier_Peak — lat :48.1125, lon :-121.1138, type : Volcano -ULTRA // 3207/2285 strato
Kawaikini — lat :22.0584, lon :-159.4974, type : Volcano -ULTRA // 1598/1598 shield
TAUPO_Volcano — lat :-38.7916, lon :175.9150, type : Volcano -ULTRA -VEI // ~1500/1500 SUPER(VEI8)
Gelai — lat :-2.6144, lon :36.1000, type : Volcano -ULTRA // 2948/1930 strato?
Kitumbeine — lat :-2.8925, lon :36.2186, type : Volcano -ULTRA // 2865/1770 strato?
San_Carlos — lat :3.3608, lon :8.5392, type : Volcano -ULTRA // 2261/1539 shield
Pico_de_Sao_Tome — lat :.2675, lon :6.543, type : Volcano -ULTRA // 2024/2024 shield
Mt.Kulal — lat :-2.7504, lon :36.9347, type : Volcano -ULTRA // 2285/1542 strato?
Pico_Basile — lat :3.5897, lon :8.7591, type : Volcano -ULTRA // 3011/3011 shield
Mt.Oku — lat :6.1833, lon :10.5167, type : Volcano -ULTRA // 3011/2491 strato
Queen_Mary’s_Peak — lat :-37.1117, lon :-12.2873, type : Volcano -ULTRA // 2062/2062 shield
Topo_da_Coroa — lat :17.0325, lon :-25.2958, type : Volcano -ULTRA // 1979/1979 strato
Pico_do_Fogo — lat :14.9494, lon :-24.3404, type : Volcano -ULTRA // 2829/2829 somma-strato
Irazu — lat :9.9792, lon :-83.8525, type : Volcano -ULTRA // 3432/1887 complex strato
Concepcion — lat :11.5397, lon :-85.6214, type : Volcano -ULTRA // 1610/1579 strato
Santa_Ana — lat :13.8554, lon :-89.6282, type : Volcano -ULTRA // 2381/1602 strato
Atitlan — lat :14.583, lon :-91.183, type : Volcano -ULTRA // 3535/1754 strato
Tajumulco — lat :15.0427, lon :-91.9045, type : Volcano -ULTRA // 4220/3980 strato
Cerro_Azul — lat :-.9200, lon :-91.4080, type : Volcano -ULTRA // 1689/1668 shield
Wolf_Volcano — lat :-.0194, lon :-91.3436, type : Volcano -ULTRA // 1707/1707 shield
Cumbre_Vieja — lat :28.5728, lon :-17.8375, type : Volcano -ULTRA // 1949/1949 strato
Pico_de_las_Nieves — lat :27.9639, lon :-15.5658, type : Volcano -ULTRA // 1949/1949 strato
Pic_Tousside — lat :21.040, lon :16.470, type : Volcano -ULTRA // 3315/1593 strato
Deriba_Caldera — lat :12.9514, lon :24.2589, type : Volcano -ULTRA // 3042/2512 shield-Cal
Karthala — lat :-11.7451, lon :43.3584, type : Volcano -ULTRA // 2361/2361 shield
Manam_Motu — lat :-4.0643, lon :145.0273, type : Volcano -ULTRA // 1807/1807 strato
Mt.Marapi — lat :-.3818, lon :100.4730, type : Volcano -ULTRA // 2891/2116 complex
Mt.Dempo — lat :-4.0158, lon :103.1283, type : Volcano -ULTRA // 3173/2450 strato
Mt.Pangrango — lat :-6.7878, lon :106.9819, type : Volcano -ULTRA // 3019/2426 strato
Mt.Sumbing — lat :-7.3850, lon :110.0725, type : Volcano -ULTRA // 3371/2577 strato
Semeru — lat :-8.1077, lon :112.9224, type : Volcano -ULTRA // 3676/3676 strato
Raung — lat :-8.1258, lon :114.0458, type : Volcano -ULTRA // 3332/3069 strato
Mt.Agung — lat :-8.3433, lon :115.5071, type : Volcano -ULTRA // 3031/3031 strato
Mount_Tambora — lat :-8.2479, lon :117.9911, type : Volcano -ULTRA -VEI // 2722/2722 strat-cal(VEI7)
Sangeang_Api — lat :-8.1961, lon :119.0700, type : Volcano -ULTRA // 1949/1949 complex
Poco_Mandasawu — lat :-8.6517, lon :120.4483, type : Volcano -ULTRA // 2370/2370 LavaDome
Iliboleng — lat :-8.3440, lon :123.2520, type : Volcano -ULTRA // 1659/1659 strato
Karangetang — lat :2.7808, lon :125.4067, type : Volcano -ULTRA // 1827/1827 strato
Ulawun — lat :-5.0588, lon :151.3308, type : Volcano -ULTRA -DECADE // 2334/2334 strato
Mt.Apo — lat :6.9875, lon :125.2710, type : Volcano -ULTRA // 2954/2954 strato
Mt.Matutum — lat :6.3606, lon :125.0747, type : Volcano -ULTRA // 2286/1950 strato
Kanlaon — lat :10.4116, lon :123.1330, type : Volcano -ULTRA // 2465/2430 strato
Bolusan — lat :12.7692, lon :124.0567, type : Volcano -ULTRA // 1565/1547 strato
Mayon — lat :14.583, lon :-91.183, type : Volcano -ULTRA // 2463/2447 strato
Mt.Isarog — lat :13.6592, lon :123.3733, type : Volcano -ULTRA // 2000/1951 strato
Mt.Labo — lat :14.0133, lon :122.7875, type : Volcano -ULTRA // 1544/1524 strato
Mt.Pinatubo — lat :15.1429, lon :120.3496, type : Volcano -ULTRA // 1486/1486:1745 strato
Mont_Orohena — lat :-17.6197, lon :-149.4842, type : Volcano -ULTRA // 2241/2241 shield? ext
Aso-San — lat :32.8869, lon :131.0841, type : Volcano -ULTRA // 1592/1592 caldera complex
Halla-San — lat :33.3617, lon :126.5292, type : Volcano -ULTRA // 1950/1950 shield
Paektu-San — lat :41.9930, lon :128.0775, type : Volcano -ULTRA // 2744/2593 strato
Kambalny — lat :51.304, lon :156.876, type : Volcano -ULTRA // 2156/1970 strato
Zhupanovsky — lat :53.5883, lon :159.1483, type : Volcano -ULTRA // 2923/2210 strato
Koryaksky — lat :53.3208, lon :158.7128, type : Volcano -ULTRA -DECADE // 3456/2999 strato
Kronotsky — lat :54.7525, lon :160.5325, type : Volcano -ULTRA // 3527/2736 strato
Tolbachik — lat :55.8308, lon :160.3258, type : Volcano —Asia -ULTRA // 3682/2190 shield-strat
Ichinsky — lat :55.6910, lon :157.7263, type : Volcano -ULTRA // 3607/3125 strato
Shiveluch — lat :56.6539, lon :161.3631, type : Volcano -ULTRA // 3307/3168 strato
Avachinsky — lat :53.2557, lon :158.8335, type : Volcano -ULTRA -DECADE // 2741/1550 strato
Veniaminof — lat :56.1983, lon :-159.3911, type : Volcano -ULTRA -VEI // 2507/2499 strato(VEI6)
Mt.Pavlof — lat :55.4203, lon :-161.8931, type : Volcano -ULTRA // 2515/2507 strato
Makushin — lat :53.8864, lon :-166.9311, type : Volcano -ULTRA // 2036/2036 strato
Maunga_Terevaka — lat :-27.0844, lon :-109.3794, type : Volcano -ULTRA // 507/Rapa-Nui shield
Domuyo — lat :-36.6397, lon :-70.433, type : Volcano -ULTRA // 4709/2229 strato
Tromen — lat :-37.1400, lon :-70.0500, type : Volcano -ULTRA // 4114/1721 strato
Llaima — lat :-38.6970, lon :-71.7300, type : Volcano -ULTRA // 3125/1819 strato
Tronador — lat :-41.1608, lon :-71.8875, type : Volcano -ULTRA // 3491/2642 strato
Maipo — lat :-34.1667, lon :-69.8333, type : Volcano -ULTRA // 5264/1900 strato
Ollague — lat :-21.3025, lon :-68.1792, type : Volcano -ULTRA // 5868/1686 strato
Guallatiri — lat :-18.4244, lon :-69.0903, type : Volcano -ULTRA // 6071/1700 strato
Parinacota — lat :-18.1633, lon :-69.1427, type : Volcano -ULTRA // 6348/1989 strato
Tacora — lat :-17.7208, lon :-69.7725, type : Volcano -ULTRA // 5980/1700 strato
Misti — lat :-16.2988, lon :-71.4057, type : Volcano -ULTRA // 5822/1785 strato
Nevado_Chachani — lat :-16.1936, lon :-71.5190, type : Volcano -ULTRA // 6057/1963 caldera
Tungurahua — lat :-1.4702, lon :-78.4448, type : Volcano -ULTRA // 5023/1554 strato
Chimborazo — lat :-1.4693, lon :-78.8169, type : Volcano -ULTRA // 6263/4118 strato
Nevado_del_Huila — lat :2.9242, lon :-76.0292, type : Volcano -ULTRA // 5364/2650 strato
Sangay — lat :-2.0142, lon :-78.3273, type : Volcano -ULTRA // 5300/1588 strato
Nevado_del_Ruiz — lat :4.8920, lon :-75.3188, type : Volcano -ULTRA // 5321/2035 strato
Cumbal — lat :-.9515, lon :-77.8879, type : Volcano -ULTRA // 4764/1575 strato
Antisana — lat :-.4868, lon :-78.1450, type : Volcano -ULTRA // 5704/1678 strato
Copiapo/Azufre — lat :-27.3060, lon :-69.1310, type : Volcano -ULTRA // 6052/1701 strato
Payun_Matru — lat :-36.4200, lon :-69.2000, type : Volcano -ULTRA // 3680/1926 shield
Lanin — lat :-39.6372, lon :-71.5024, type : Volcano -ULTRA // 3776/2624 strato
Mt.Murphy — lat :-75.333, lon :-110.733, type : Volcano -ULTRA // 2705/2055 shield
Mawson_Peak — lat :-53.1032, lon :73.5161, type : Volcano -ULTRA // 2745/2745 complex
Mt.Melbourne — lat :-74.35, lon :164.7, type : Volcano -ULTRA // 2730/1699 strato
Mt.Morning — lat :-78.517, lon :163.583, type : Volcano -ULTRA // 2725/1515 shield
Mt.Discovery — lat :-78.367, lon :165.017, type : Volcano -ULTRA // 2681/1637 strato
Mt.Andrus — lat :-75.8, lon :-132.3, type : Volcano -ULTRA // 2978/???? shield
Mt.Vesuvius — lat :40.817, lon :14.433, type : Volcano -DECADE // 1281m somma-strato
Mt.Merapi — lat :-7.5407, lon :110.4457, type : Volcano -DECADE // 2930/1356
Galeras — lat :1.2219, lon :-77.3592, type : Volcano -DECADE // 4276/???? strato
Taal — lat :14.0113, lon :120.9977, type : Volcano -DECADE // 311/311 complex
Sakurajima — lat :31.5833, lon :130.6500, type : Volcano -DECADE // 1117/1117 strato
Unzen — lat :32.7577, lon :130.3015, type : Volcano -DECADE // 1500/???? complex-strato
Santa_Maria — lat :14,7571, lon :-91.5517, type : Volcano -DECADE // 3772/1054 LavaDome
Santorini — lat :36.3956, lon :25.4592, type : Volcano -DECADE // submarine caldera
Krakatoa_Anak — lat :-6.0993, lon :105.4215, type : Volcano -DECADE -VEI // 813 /VEI6 caldera
Cerro_Blanco — lat :-26.7603, lon :-67.7414, type : Volcano -VEI // 4670/VEI7 strato
Ile_Amsterdam — lat :-37.8494, lon :77.5494, type : Volcano —ISOLATION // 867/867
Table-7: IMPACT CRATERS
DIAMETER (kms) AGE (Millions of Years)
1.Vredefort — lat :-27.000, lon :27.500, type : ImpactCrater // 300 2023 ± 4
2.Sudbury — lat :46.600, lon :-81.183, type : ImpactCrater // 250 1850 ± 3
3.Chicxulub — lat :21.333, lon :-89.500, type : ImpactCrater // 180 64.98 ± .05
4.Popigai — lat :71.650, lon :111.183, type : ImpactCrater // 100 35.7 ± .2
5.Manicouagan — lat :51.383, lon :-68.700, type : ImpactCrater // 100 214 ± 1
6.Acraman — lat :-32.017, lon :135.450, type : ImpactCrater // 90 580
7.ChesapeakeBay — lat :37.283, lon :-76.017, type : ImpactCrater // 85 35.5 ± .3
8.Phuchezh-Katunki — lat :56.967, lon :43.717, type : ImpactCrater // 80 167 ± 3
9.Morokweng — lat :-26.467, lon :23.533, type : ImpactCrater // 70 145 ± .8
10.Kara — lat :69.100, lon :64.150, type : ImpactCrater // 65 70.3 ± 2.2
11.Beaverhead — lat :44.250, lon :-114.000, type : ImpactCrater // 60 600
12.Woodleigh — lat :-26.050, lon :114.667, type : ImpactCrater // 60-160 364
13.Tookoonooka — lat :-27.117, lon :142.833, type : ImpactCrater // 55 128 ± 5
14.Charveloix — lat :47.533, lon :-70.300, type : ImpactCrater // 54 342 ± 15
15.SiljanRing — lat :61.033, lon :14.867, type : ImpactCrater // 52 376.8 ± 1.7
16.Karakul — lat :39.017, lon :73.450, type : ImpactCrater // 52 25
17.Montagnais — lat :42.883, lon :-64.217, type : ImpactCrater // 45 50.5 ± .76
18.Araguainha — lat :-16.783, lon :-52.983, type : ImpactCrater // 40 244.4 ± 3.25
19.Mjolnir — lat :73.800, lon :29.667, type : ImpactCrater // 40 142 ±2.6
20.SaintMartin — lat :51.783, lon :-98.533, type : ImpactCrater // 40 220 ± 32
21.Carswell — lat :58.450, lon :-109.500, type : ImpactCrater // 39 115 ± 10
22.ClearwaterWest — lat :56.217, lon :-74.500, type : ImpactCrater // 36 290 ± 20
23.Manson — lat :42.583, lon :-94.550, type : ImpactCrater // 35 73.8 ± .3
24.Saqqar — lat :29.583, lon :38.700, type : ImpactCrater // 34 70-410
25.SlateIslands — lat :48.667, lon :-87.000, type : ImpactCrater // 30 450
26.Yarrabubba — lat :-27.167, lon :118.833, type : ImpactCrater // 30 ~2000
27.Keurusselka — lat :62.133, lon :24.600, type : ImpactCrater // 30 1400-1500
28.Shoemaker — lat :-25.867, lon :120.883, type : ImpactCrater // 30 1630
29.Mistatin — lat :55.883, lon :-63.300, type : ImpactCrater // 28 36.4 ± 4
30.ClearwaterEast — lat :56.067, lon :-74.100, type : ImpactCrater // 26 290 ± 20
31.Kamensk — lat :48.350, lon :40.500, type : ImpactCrater // 25 49 ± .2
32.SteenRiver — lat :59.500, lon :-117.633, type : ImpactCrater // 25 91 ± 7
33.Strangways — lat :-15.200, lon :133.583, type : ImpactCrater // 25 646 ± 42
34.Tunnunik — lat :72.467, lon :-113.933, type : ImpactCrater // 25 130-350
35.Boltysh — lat :48.900, lon :32.250, type : ImpactCrater // 24 65.17
36.NordlingerRies — lat :48.883, lon :10.567, type : ImpactCrater // 24 14.3-14.5
37.Presqu’ile — lat :49.717, lon :-74.800, type : ImpactCrater // 24 <500
38.Haughton — lat :75.383, lon :-89.667, type : ImpactCrater // 23 39
39.Lappajarvi — lat :63.200, lon :23.700, type : ImpactCrater // 23 73.3 ± 5.3
40.Rochechouart — lat :45.82417, lon :0.78167, type : ImpactCrater // 23 214 ± 8
41.GossesBluff — lat :-23.82083, lon :132.30778, type : ImpactCrater // 22 142.5 ± .8
42.AmeliaCreek — lat :-20.917, lon :134.833, type : ImpactCrater // 20 600-1660
43.Logancha — lat :65.517, lon :95.933, type : ImpactCrater // 20 40 ± 20
44.Obolon — lat :49.583, lon :32.917, type : ImpactCrater // 20 169 ± 7
45.Glikson — lat :-23.983, lon :121.567, type : ImpactCrater // 19 < 508
46.Dellen — lat :61.850, lon :16.700, type : ImpactCrater // 19 89 ± 2.7
47.Oasis — lat :24.583, lon :24.400, type : ImpactCrater // 18
48.LawnHill — lat :-18.667, lon :138.650, type : ImpactCrater // 18 > 515
49.El’gygytgyn — lat :67.500, lon :172.083, type : ImpactCrater // 18 3.5 ± .5
50.Luizi — lat :-10.167, lon :28.000, type : ImpactCrater // 17
51.Suavjarvi — lat :63.117, lon :33.383, type : ImpactCrater // 16 2400
52.Ames — lat :36.250, lon :-98.200, type : ImpactCrater // 16 470 ± 30
53.Logoisk — lat :54.200, lon :27.800, type : ImpactCrater // 15 42.3 ± 1.1
54.Kaluga — lat :54.500, lon :36.200, type : ImpactCrater // 15 380 ± 5
55.Zhamanshin — lat :48.400, lon :60.967, type : ImpactCrater // 14 .900 ± .1
56.Janisjarvi — lat :61.967, lon :30.917, type : ImpactCrater // 14 700 ± 5
57.Gweni-Fada — lat :17.417, lon :21.750, type : ImpactCrater // 14
58.Spider — lat :-16.733, lon :126.083, type : ImpactCrater // 13
59.SierraMadera — lat :30.600, lon :-102.917, type : ImpactCrater // 13
60.Kentland — lat :40.750, lon :-87.400, type : ImpactCrater // 13
61.DeepBay — lat :56.400, lon :-102.983, type : ImpactCrater // 13 99 ± 4
62.Marquez — lat :31.283, lon :-96.300, type : ImpactCrater // 12.7 58 ± 2
63.Aorounga — lat :19.100, lon :19.250, type : ImpactCrater // 12.6
64.Nicholson — lat :62.667, lon :-102.683, type : ImpactCrater // 12.5
65.WellsCreek — lat :36.383, lon :-87.667, type : ImpactCrater // 12 200 ± 100
66.VargeaoDome — lat :-26.833, lon :-52.117, type : ImpactCrater // 12
67.SerraDaCangalha — lat :-8.083, lon :-46.867, type : ImpactCrater // 12
68.Avak — lat :71.250, lon :-156.500, type : ImpactCrater // 12
69.Ternovka — lat :48.133, lon :33.517, type : ImpactCrater // 11 280 ± 10
70.Dhala — lat :25.300, lon :78.133, type : ImpactCrater // 11 1700-2100
71.Bosumtwi — lat :6.5050, lon :-1.4083, type : ImpactCrater // 10.5 1.07
72.SantaMarta — lat :-10.167, lon :-45.250, type : ImpactCrater // 10 66-100
73.UpheavalDome — lat :38.433, lon :-109.933, type : ImpactCrater // 10
74.Paasselka — lat :62.150, lon :29.417, type : ImpactCrater // 10 1800
75.KellyWest — lat :-19.933, lon :133.950, type : ImpactCrater // 10 >550
76.Karla — lat :54.917, lon :48.033, type : ImpactCrater // 10 5 ± 1
77.Flaxman — lat :-34.617, lon :139.067, type : ImpactCrater // 10 > 35
78.EagleButte — lat :49.700, lon :-110.500, type : ImpactCrater // 10
79.VistaAlegre — lat :-25.950, lon :-52.683, type : ImpactCrater // 9.5
80.RedWing — lat :47.600, lon :-103.550, type : ImpactCrater // 9 200 ± 25
81.Ragonzika — lat :58.733, lon :61.800, type : ImpactCrater // 9 46 ± 3
82.Mien — lat :56.417, lon :14.867, type : ImpactCrater // 9 121 ± 2.3
83.Lumparn — lat :60.150, lon :20.100, type : ImpactCrater // 9 1000
84.ConnollyBasin — lat :-23.533, lon :124.750, type : ImpactCrater // 9
85.Ilyinets — lat :49.117, lon :29.100, type : ImpactCrater // 8.5 378 ± 5
86.Crawford — lat :-34.717, lon :139.033, type : ImpactCrater // 8.5 > 35
87.Calvin — lat :41.833, lon :-85.950, type : ImpactCrater // 8.5 450 ± 10
88.Vepriai — lat :55.083, lon :24.583, type : ImpactCrater // 8 160 ± 10
89.SerpentMound — lat :39.033, lon :-83.400, type : ImpactCrater // 8
90.Neugrund — lat :59.333, lon :23.667, type : ImpactCrater // 8 470
91.LaMoinerie — lat :57.433, lon :-66.617, type : ImpactCrater // 8 450 ± 50
92.GloverBluff — lat :43.967, lon :-89.533, type : ImpactCrater // 8
93.Elbow — lat :50.983, lon :-106.717, type : ImpactCrater // 8 395 ± 25
94.DesPlaines — lat :42.050, lon :-87.867, type : ImpactCrater // 8
95.Couture — lat :60.133, lon :-75.333, type : ImpactCrater // 8 430 ± 25
96.Bigach — lat :48.567, lon :82.017, type : ImpactCrater // 8 5
97.Beyenchime-Salaatin — lat :71.000, lon :121.667, type : ImpactCrater // 8 40 ± 20
98.Wanapitei — lat :46.750, lon :-80.750, type : ImpactCrater // 7.5 37.2 ± 1.2
99.MattWilson — lat :-15.50111, lon :131.17861, type : ImpactCrater // 7.5
100.Lockne — lat :63.000, lon :14.817, type : ImpactCrater // 7.5 458
101.Piccaninny — lat :-17.433, lon :128.433, type : ImpactCrater // 7
102.CrookedCreek — lat :37.833, lon :-91.383, type : ImpactCrater // 7 320 ± 80
103.CloudCreek — lat :43.117, lon :-106.750, type : ImpactCrater // 7 190 ± 30
104.Soderfjarden — lat :63.000, lon :21.567, type : ImpactCrater // 6.6 ~600
105.SantaFe — lat :35.750, lon :-105.933, type : ImpactCrater // 6-13
106.TinBider — lat :27.600, lon :5.117, type : ImpactCrater // 6
107.Saaksjarvi — lat :61.400, lon :22.400, type : ImpactCrater // 6 ~560
108.RockElm — lat :44.717, lon :-92.233, type : ImpactCrater // 6
109.Pilot — lat :60.283, lon :-111.000, type : ImpactCrater // 6 445 ± 2
110.Middlesboro — lat :36.617, lon :-83.733, type : ImpactCrater // 6
111.MapleCreek — lat :49.800, lon :-109.100, type : ImpactCrater // 6
112.Kursk — lat :51.700, lon :36.000, type : ImpactCrater // 6 250 ± 80
113.Foelsche — lat :-16.667, lon :136.783, type : ImpactCrater // 6 > 545
114.Decaturville — lat :37.900, lon :-92.717, type : ImpactCrater // 6
115.Chukcha — lat :75.700, lon :97.800, type : ImpactCrater // 6 < 70
116.JabalWaqfEsSwwan — lat :31.050, lon :36.800, type : ImpactCrater // 5.5 37-56
117.Chiyli — lat :49.167, lon :57.850, type : ImpactCrater // 5.5 46 ± 7
118.GoatPaddock — lat :-18.333, lon :126.667, type : ImpactCrater // 5.1
119.Mizarai — lat :54.017, lon :23.900, type : ImpactCrater // 5 500 ± 20
120.GowLake — lat :56.450, lon :-104.483, type : ImpactCrater // 5
121.Gardnos — lat :60.650, lon :9.000, type : ImpactCrater // 5 500 ± 10
122.Wetumpka — lat :32.517, lon :-86.167, type : ImpactCrater // 4.7 ~83
123.RioCuarto — lat :-32.8783, lon :-64.2233, type : ImpactCrater // 4.5
124.RiachaoRing — lat :-7.717, lon :-46.650, type : ImpactCrater // 4.5
125.Dobele — lat :56.583, lon :23.250, type : ImpactCrater // 4.5 290 ± 35
126.SuvasvesiNorth — lat :62.700, lon :28.167, type : ImpactCrater // 4 < 1000
127.MountToondina — lat :-27.950, lon :135.367, type : ImpactCrater // 4
128.Kardla — lat :59.017, lon :22.767, type : ImpactCrater // 4 455
129.IleRouleau — lat :50.683, lon :-73.883, type : ImpactCrater // 4
130.Glasford — lat :40.600, lon :-89.783, type : ImpactCrater // 4
131.SuvasvesiSouth — lat :62.600, lon :28.217, type : ImpactCrater // 3.8 ~250
132.Steinheim — lat :48.683, lon :10.067, type : ImpactCrater // 3.8 15 ± 1
133.FlynnCreek — lat :36.283, lon :-85.667, type : ImpactCrater // 3.8 360 ± 20
134.Brent — lat :46.083, lon :-78.483, type : ImpactCrater // 3.8 396 ± 20
135.Colonia — lat :-23.933, lon :-68.283, type : ImpactCrater // 3.6 > 5
136.ZelenyGai — lat :48.067, lon :32.750, type : ImpactCrater // 3.5 80 ± 20
137.Oarkziz — lat :29.000, lon :-7.550, type : ImpactCrater // 3.5
138.Kgagodi — lat :-22.483, lon :27.583, type : ImpactCrater // 3.5
139.Pingualuit — lat :61.283, lon :-73.667, type : ImpactCrater // 3.44 1.4 ± .1
140.Zapadnaya — lat :49.733, lon :29.000, type : ImpactCrater // 3.2 165 ± 5
141.Newporte — lat :48.967, lon :-101.967, type : ImpactCrater // 3.2
142.Agoudal — lat :31.983, lon :-5.500, type : ImpactCrater // 3 .105
143.Iso-Naakkima — lat :62.183, lon :27.150, type : ImpactCrater // 3 1000
144.Gusev — lat :48.433, lon :40.533, type : ImpactCrater // 3 49 ± .2
145.Grandby — lat :58.417, lon :14.933, type : ImpactCrater // 3 443-470
146.Goyder — lat :-13.150, lon :135.033, type : ImpactCrater // 3
147.Shunak — lat :47.217, lon 72.767, type : ImpactCrater // 2.8 45 ± 10
148.Rotmistrovka — lat :49.000, lon :32.000, type : ImpactCrater // 2.7 120 ± 10
149.Ritland — lat :59.233, lon :6.433, type : ImpactCrater // 2.7 520 ± 20
150.Viewfield — lat :49.583, lon :-103.067, type : ImpactCrater // 2.5 190 ± 20
151.RoterKamm — lat :-27.767, lon :16.300, type : ImpactCrater // 2.5 3.7 ± .3
152.MishinaGora — lat :58.717, lon :28.050, type : ImpactCrater // 2.5 300 ± 50
153.WestHawk — lat :49.767, lon :-95.183, type : ImpactCrater // 2.44 351 ± 20
154.Holleford — lat :44.467, lon :-76.633, type : ImpactCrater // 2.35 550 ± 100
155.Tvaren — lat :58.767, lon :17.417, type : ImpactCrater // 2 455
156.B.P.Structure — lat :25.317, lon :24.317, type : ImpactCrater // 2
157.Tenoumer — lat :22.91806, lon :-10.40750, type : ImpactCrater // 1.9 .021 ± .01
158.Lonar — lat :19.967, lon :76.517, type : ImpactCrater // 1.83 .052 ±6k
159.Xiuyan — lat :40.350, lon :123.450, type : ImpactCrater // 1.8 .050
160.Talemzane — lat :33.317, lon :4.033, type : ImpactCrater // 1.75
161.Liverpool — lat :-12.400, lon :134.050, type : ImpactCrater // 1.6 543-1000
162.Saarijarvi — lat :65.283, lon :28.383, type : ImpactCrater // 1.5 > 600
163.Karikkoselka — lat :62.217, lon :25.250, type : ImpactCrater // 1.5 230
164.Tabun-Khara-Obo — lat :44.133, lon :109.650, type : ImpactCrater // 1.3 150 ± 20
165.Hummeln — lat :57.367, lon :16.250, type : ImpactCrater // 1.2 443-470
166.Barringer — lat :35.033, lon :-111.017, type : ImpactCrater // 1.19 .049 ± .003
167.Tswaing — lat :-25.40833, lon :28.08278, type : ImpactCrater // 1.13 .220 ± .05
168.Malingen — lat :62.917, lon :14.550, type : ImpactCrater // 1 458
169.WolfeCreek — lat :-19.167, lon :127.800, type : ImpactCrater // 0.875 .3
170.Kalkkop — lat :-32.717, lon :24.433, type : ImpactCrater // 0.64 .25
171.Monturaqui — lat :-23.933, lon :-68.267, type : ImpactCrater // 0.46
172.Amguid — lat :26.083, lon :4.400, type : ImpactCrater // 0.45
173.Aouelloul — lat :20.250, lon :-12.683, type : ImpactCrater // 0.39 3 ± .3
174.Macha — lat :60.100, lon :117.583, type : ImpactCrater // 0.3 ~5300 B.C.
175.Boxhole — lat :-22.617, lon :135.200, type : ImpactCrater // 0.17 ~3400 B.C.
176.Odessa — lat :31.750, lon :-102.483, type : ImpactCrater // 0.168
177.Henbury — lat :-24.567, lon :133.133, type : ImpactCrater // 0.157 ~2200 B.C.
178.Wabar — lat :21.500, lon :50.467, type : ImpactCrater // 0.116 ?
179.Kaalijarv — lat :58.367, lon :22.667, type : ImpactCrater // 0.11 ~2000 B.C.
180.Morasko — lat :52.483, lon :16.900, type : ImpactCrater // 0.1 ~3000 B.C.
181.Veevers — lat :-22.967, lon :125.367, type : ImpactCrater // 0.08
182.Ilumetsa — lat :57.967, lon :27.417, type : ImpactCrater // 0.08 > .0066
183.Sobolev — lat :46.300, lon :137.867, type : ImpactCrater // 0.053
184.CampoDelCielo — lat :-27.633, lon :-61.700, type : ImpactCrater // 0.05 ~2000 B.C.
185.Kamil — lat :22.01833, lon :26.08750, type : ImpactCrater // 0.045
186.Whitecourt — lat :54.000, lon :-115.600, type : ImpactCrater // 0.036
187.Sikhote-Alin — lat :46.117, lon :134.667, type : ImpactCrater // 0.027 69
188.Dalgaranga — lat :-27.633, lon :117.283, type : ImpactCrater // 0.024 ?
189.Haviland — lat :37.583, lon :-99.167, type : ImpactCrater // 0.015
Table-8: Nazca Lines-Great Circles Data
Radial Center Locations
Tiwanaku (Akapana): lat: -16.5564, lon: -68.6728
Cape Agulhas: lat: -34.839, lon: 20.004
Geodesic Antipode to Cape Agulhas: lat: 34.839, lon: -159.996
Amazon River Delta: lat: 0, lon: -50
Rapa-Nui (Easter Island): lat: -27.109, lon: -109.366
Tiwanaku Great Circles Angles
Line/Great Circle Angle to True
Name Tiwanaku Orient Heading
T0 (Tiwanaku Orient) 0 90
T1 4 86
T2 26.16 63.84
T3 53.54 36.46
T4 81.57 8.43
T5 97.04 352.96
T6 106.65 343.35
T7 118.94 331.06
T8 142.08 307.92
T9 187.64 262.36
T10 199.44 250.56
T11 219.17 230.83
T12 256.09 193.91
T13 308.86 141.14
Cape Agulhas Great Circles Angles
Line/Great Circle Angle to True
Name Primary C-A Heading
C-A (Primary) 0 281.31655
Antipodal Orient 0 90
C1 6.94 288.68345
C2 9.41 291.15345
C3 10.32 292.06345
C4 11.11 292.85345
C5 11.65 293.39345
C6 13.82 295.56345
C7 21.14 301.88345
C8 24.73 306.47345
C9 26.35 308.09345
C10 28.25 310.09345
C11 32.02 313.76345
C12 37.63 319.37345
C13 38.47 320.21345
C14 40.38 322.12345
C15 43.37 325.11345
C16 44.62 326.36345
C17 47.99 329.73345
C18 49.12 330.86345
C19 54.79 336.53345
C20 59.63 341.37345
C21 62.85 344.49345
C22 66.35 348.09345
C23 76.42 358.16345
C24 78.74 0.49345
C25 -5.31 276.43345
Amazon River Delta Great Circles Angles
Line/Great Circle Angle to True
Name Primary A-C Heading
Primary A-C 0 126.52655
A1 33.19 93.33655
A2 39.76 86.76655
A3 47.43 79.09655
A4 50.83 75.69655
A5 61.30 65.22655
A6 96.28 30.24655
A7 99.9 26.62655
A8 121.5 5.02655
A9 127.72 358.80655
A10 191.33 295.19655
A11 204 282.52655
A12 273.58 212.94655
A13 301.52 185.00655
A14 334.64 151.88655
Geodetic Antipode (Cape Agulhas) Great Circles Angles
Line/Great Circle Angle to True
Name Primary G-A Heading
G-A (Primary) 0 135.34894
G1 8.84 126.50894
G2 31.77 103.57894
G3 41.93 93.41894
G4 49.72 85.62894
G5 52.9 82.44894
G6 64.73 70.61894
G7 70.61 64.73894
G8 101.14 34.20894
G9 129.69 5.65894
G10 153.45 341.89894
G11 171.48 323.86894
G12 191.61 303.73894
G13 210.69 284.65894
G14 228.2 267.14894
G15 246.07 249.27894
G16 258.65 236.69894
G17 263.01 232.33894
G18 268.38 226.96894
G19 287.12 208.22894
G20 325.75 169.59894
G21 342.65 152.69894
Rapa-Nui (Easter Island) Great Circles Angles
Line/Great Circle Angle to True
Name Primary R-A Heading
R-A (Primary) 0 74.8981
R1 61.39 13.5081
By Frank Maglione Nicholson (concept development, statistical analysis, graphics), Ken Phungrasamee (concept development, graphics, simulation testing) and David Grimason (concept development, programming, statistical analysis).
A huge thank you also to the following people for their invaluable contributions:
- Jim Alison for his contribution to the concept development, as described above.
- Sharif Sakr for his advice on presentation.
- Nathan Johnson for his help with research.
- Graham Hancock and Robert Bauval, whose works inspired this one.
- And all the other friends and family members, who have helped along the way.
For the latest updates and new material, please visit nazcasolution.com







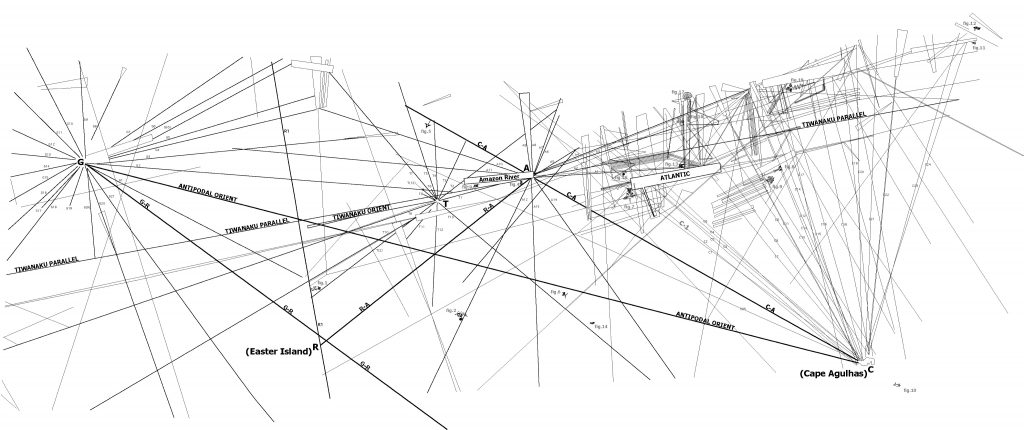




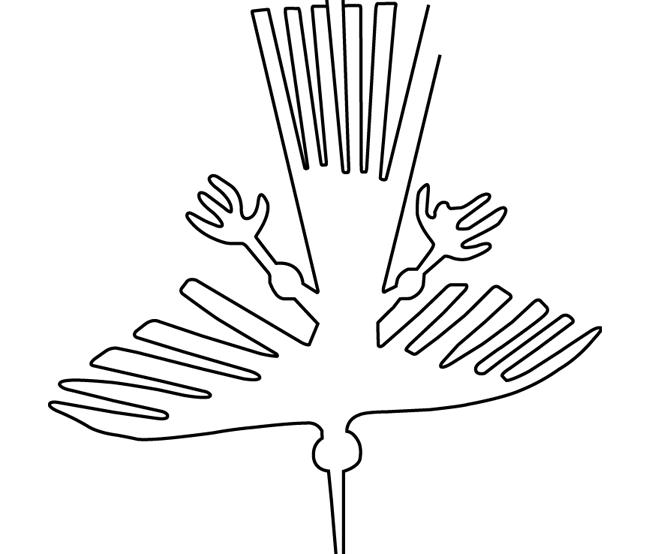

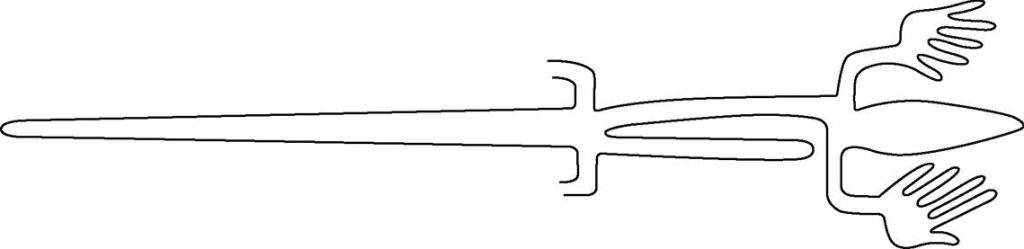
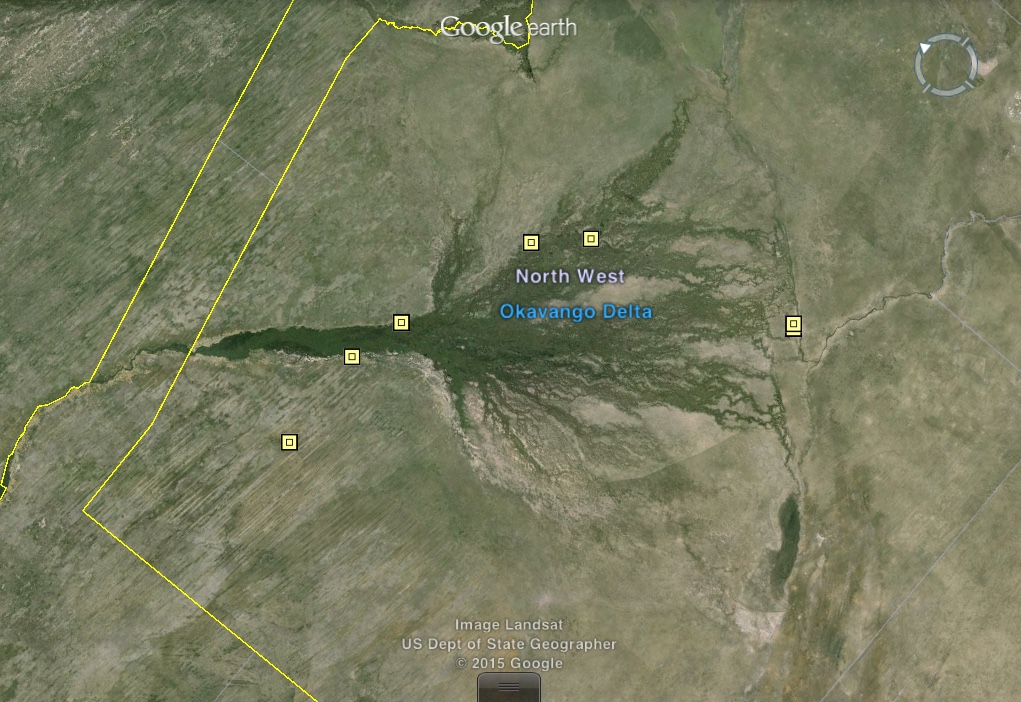

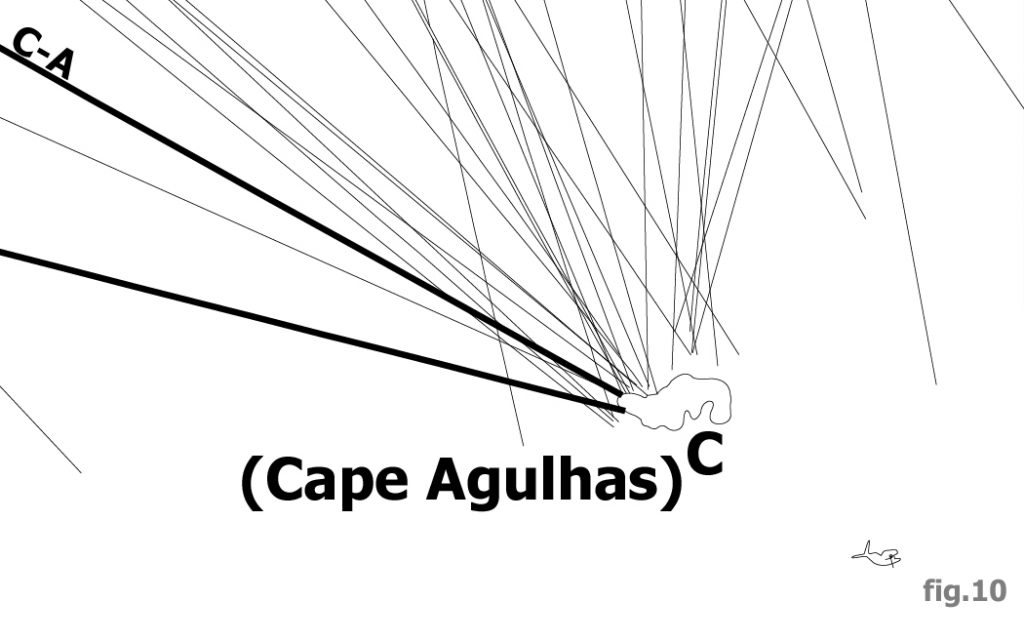

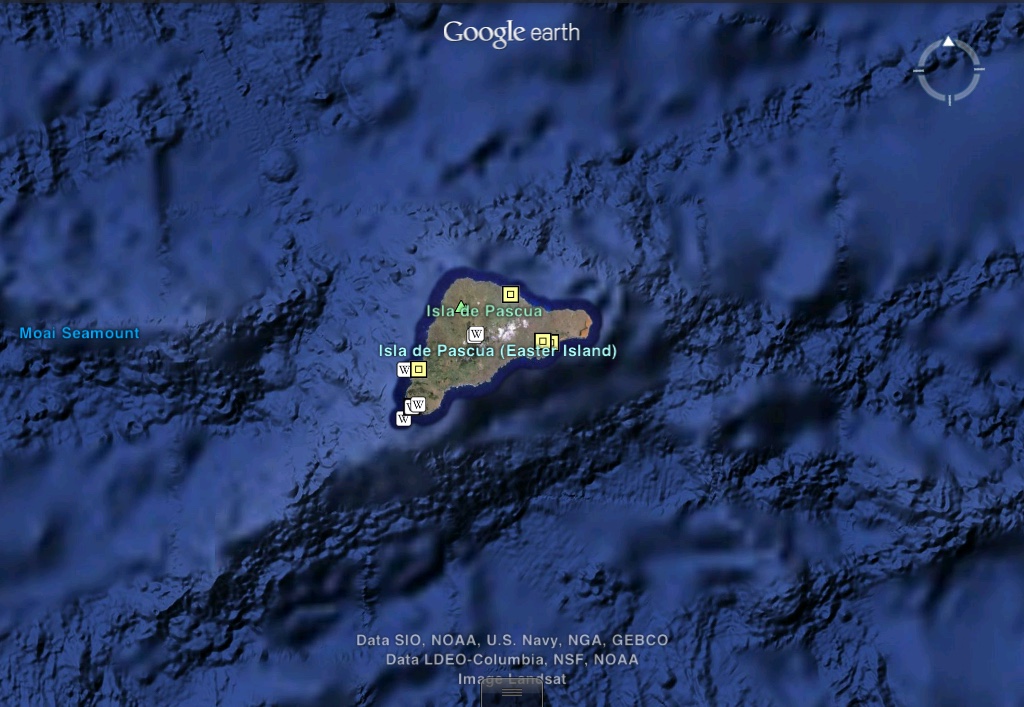
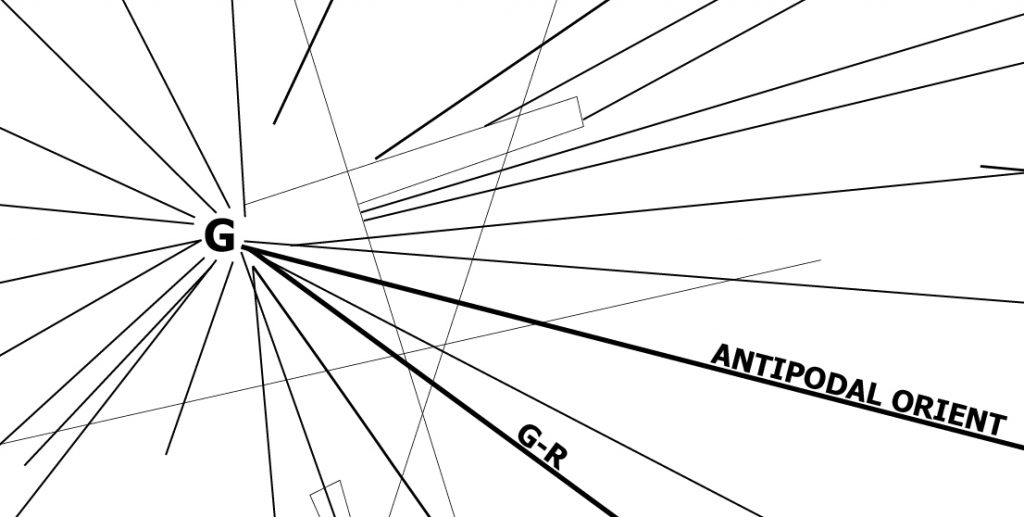

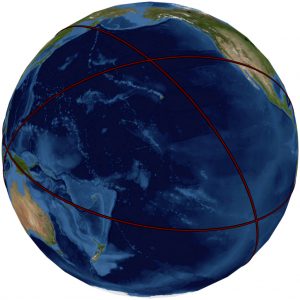

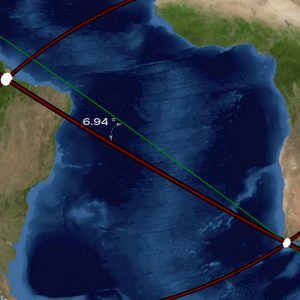
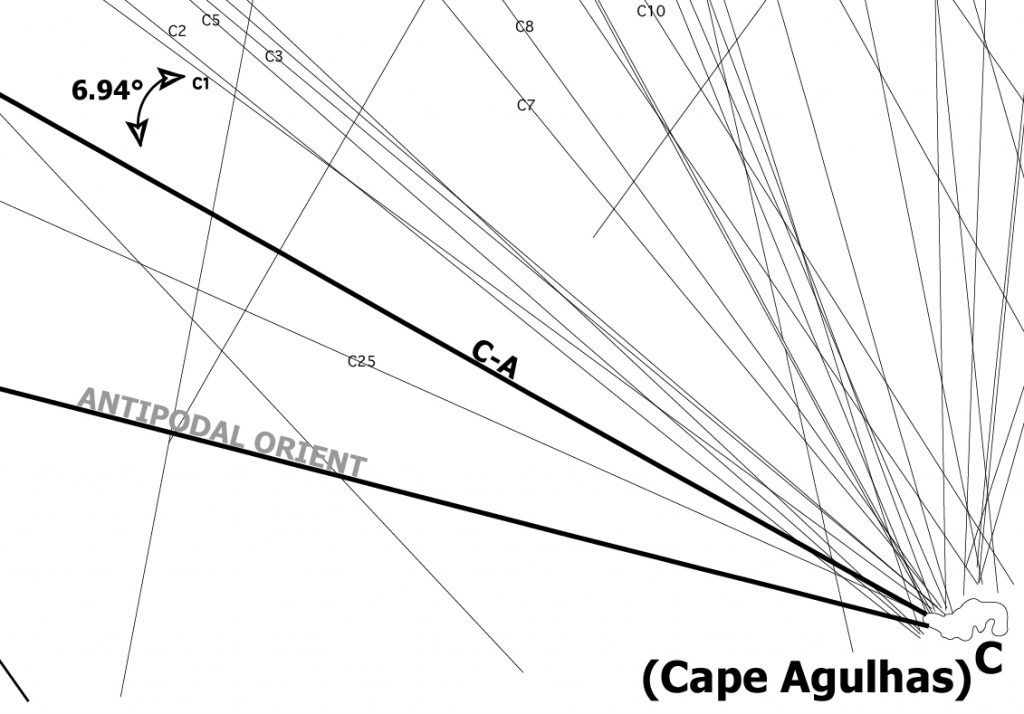
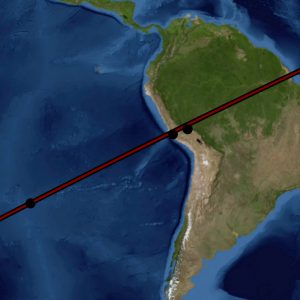
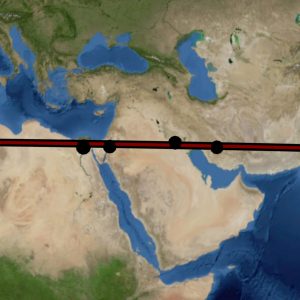
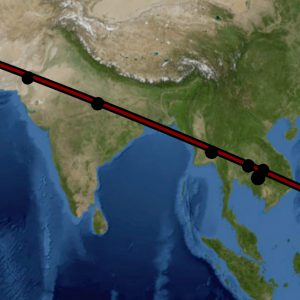

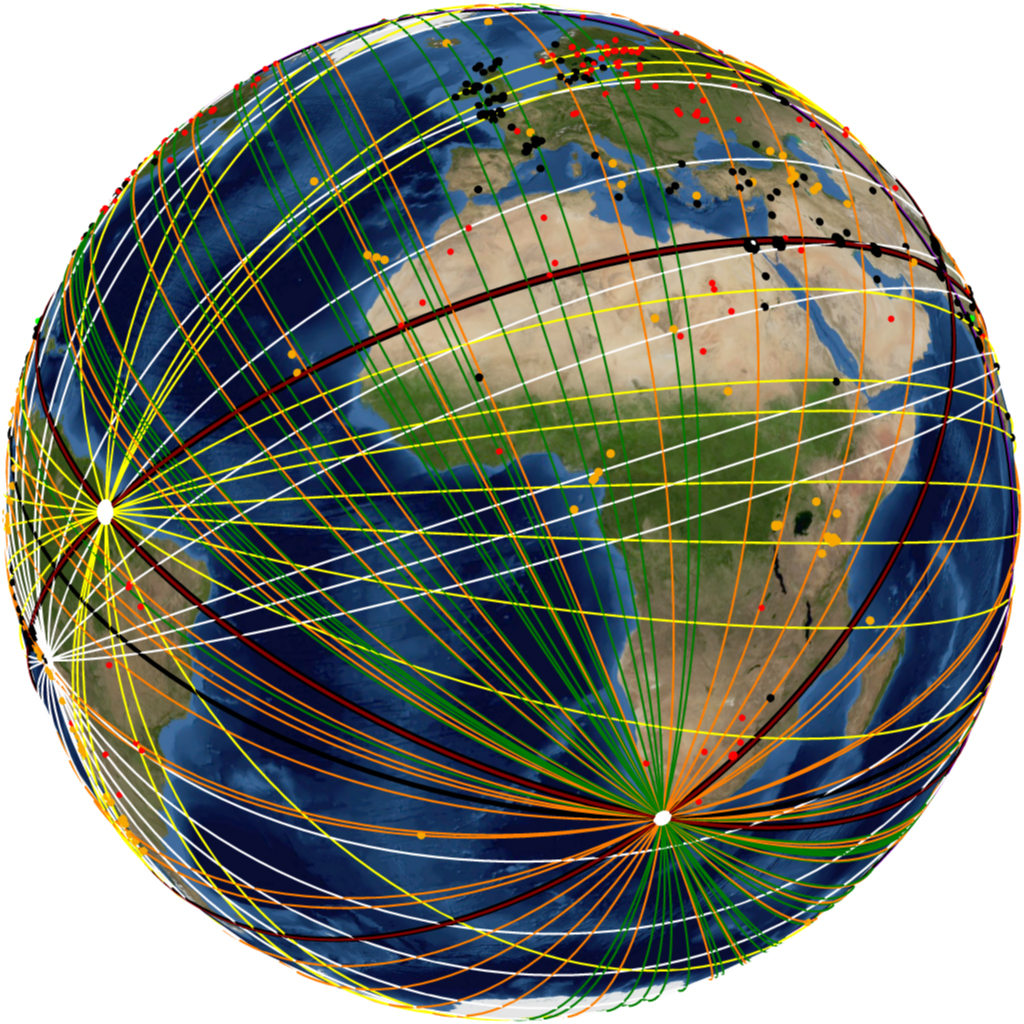


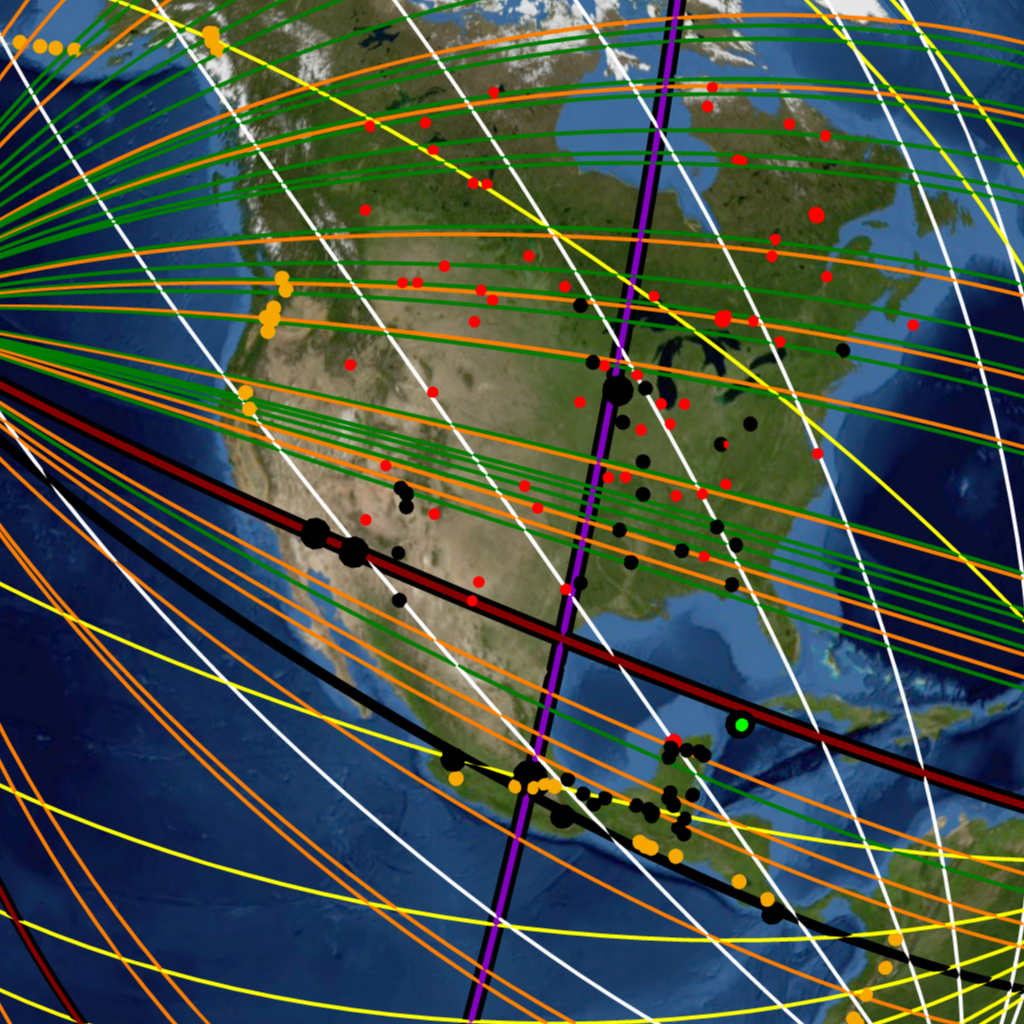

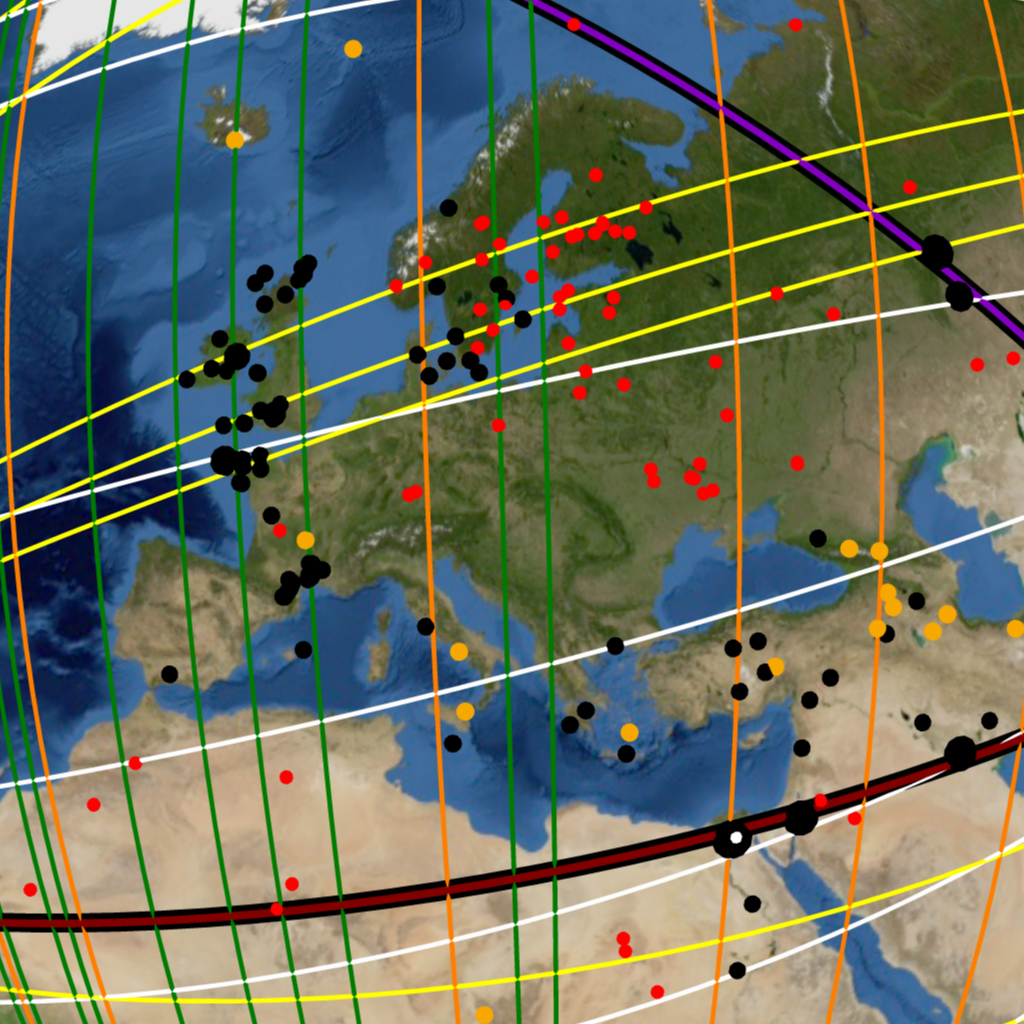
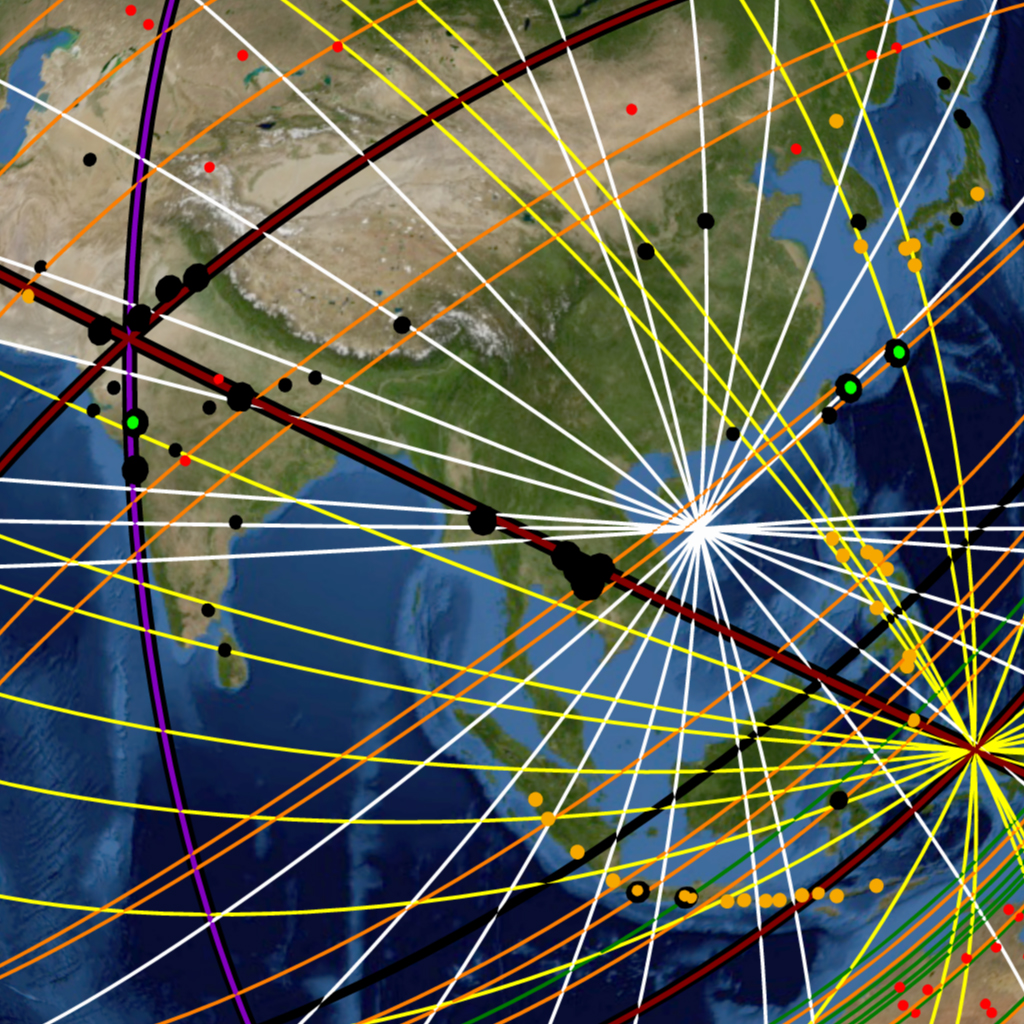
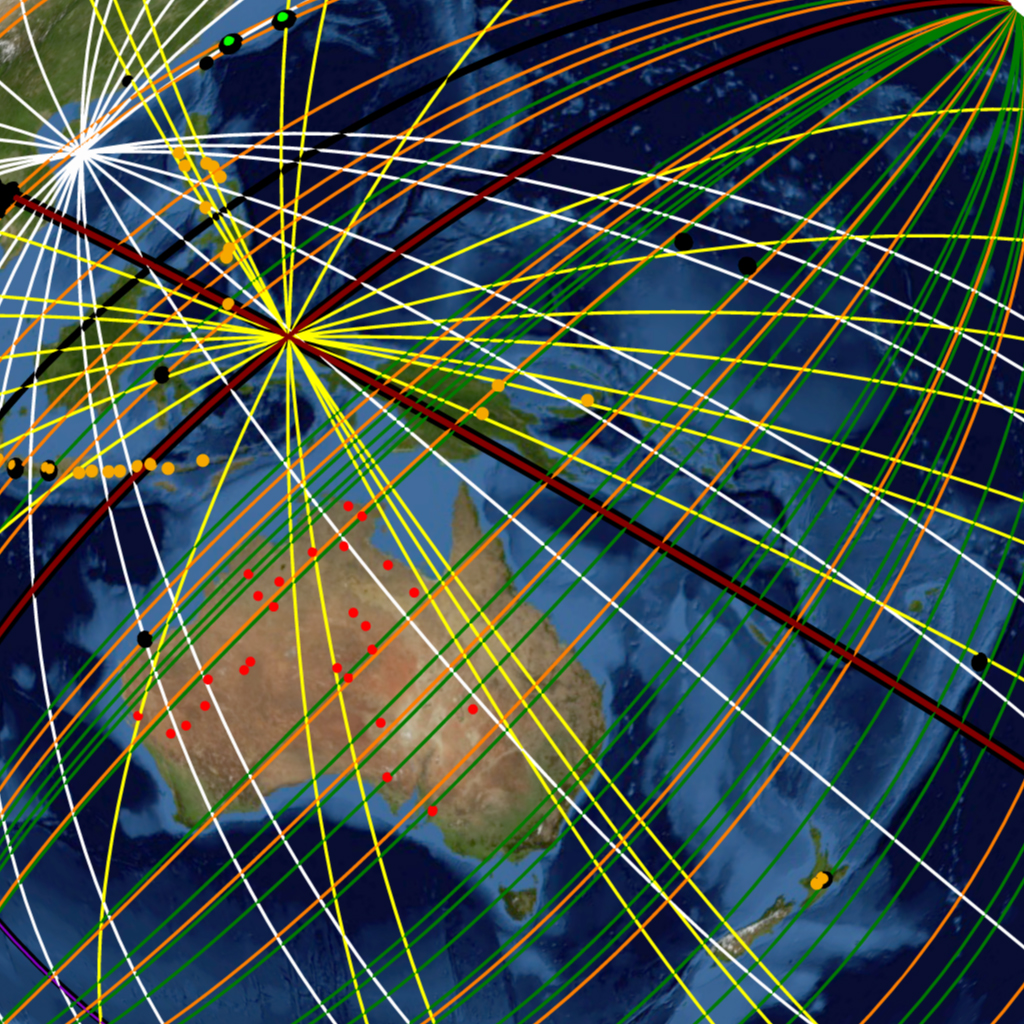
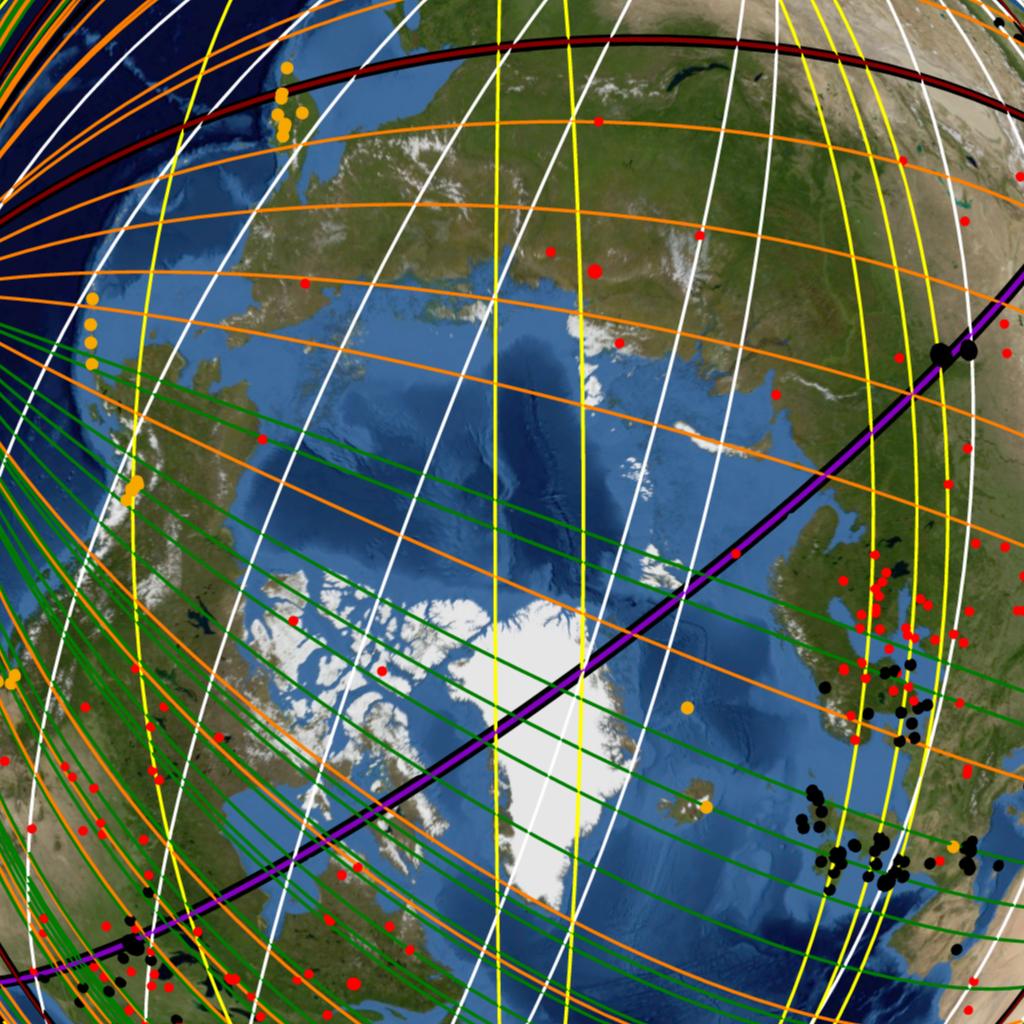

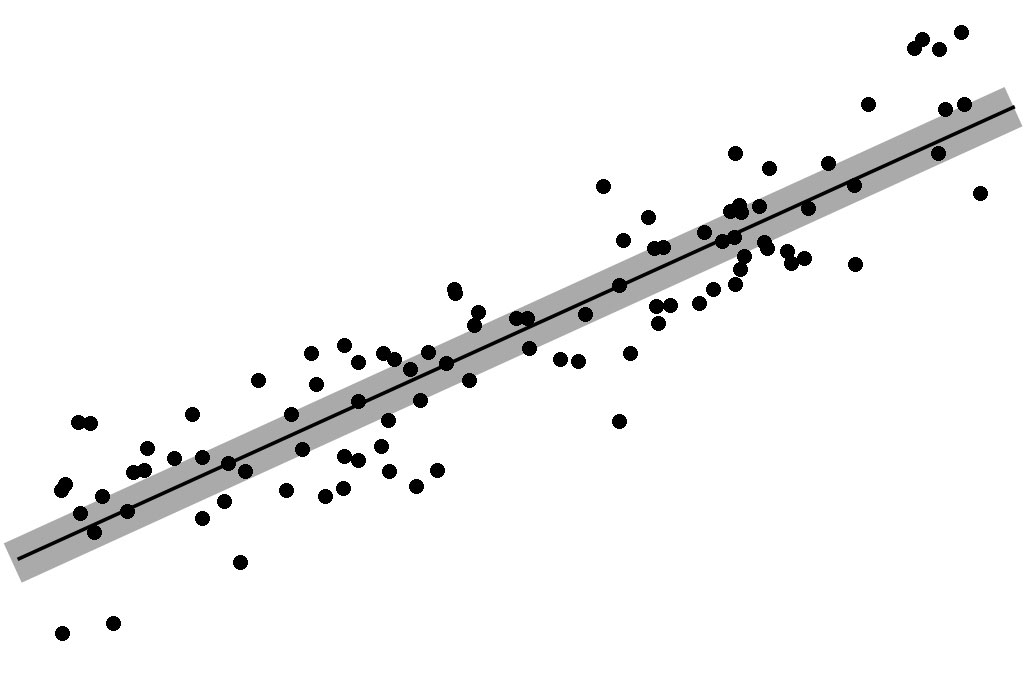
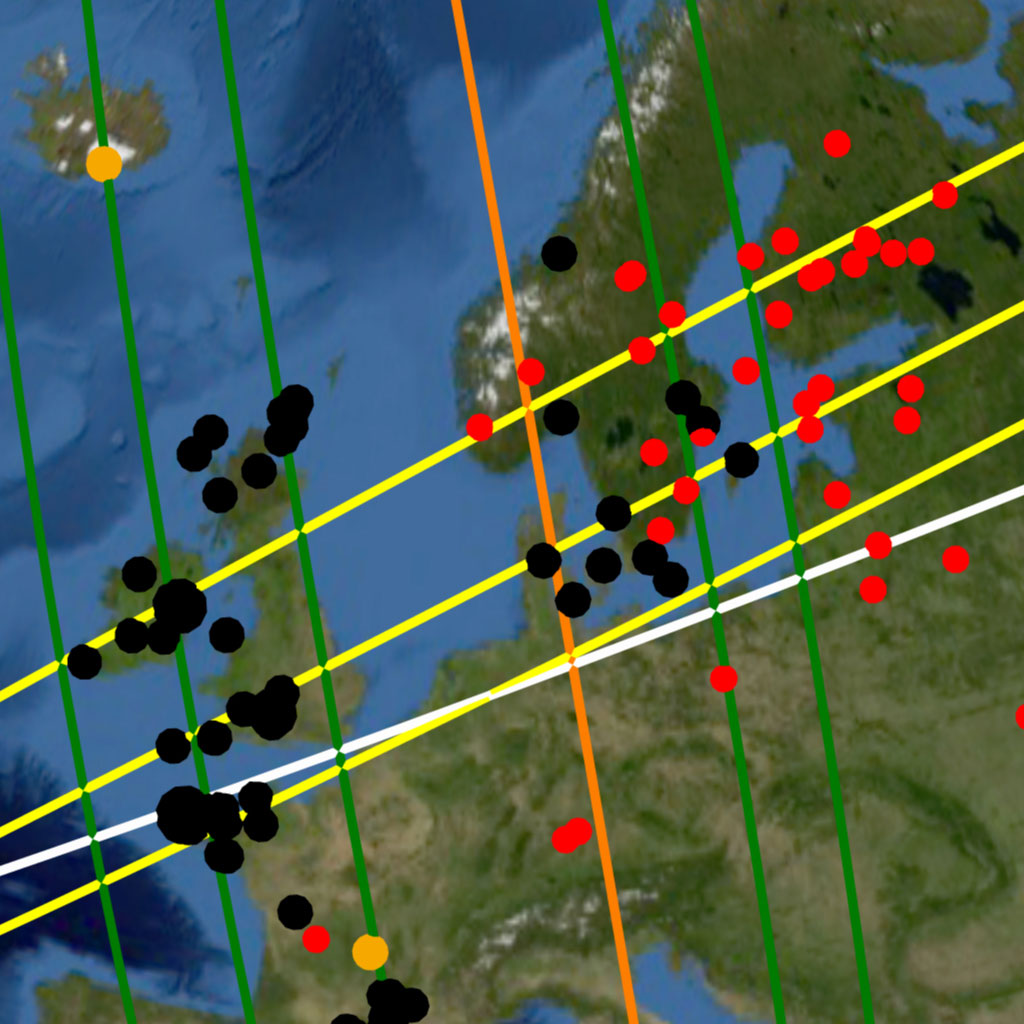
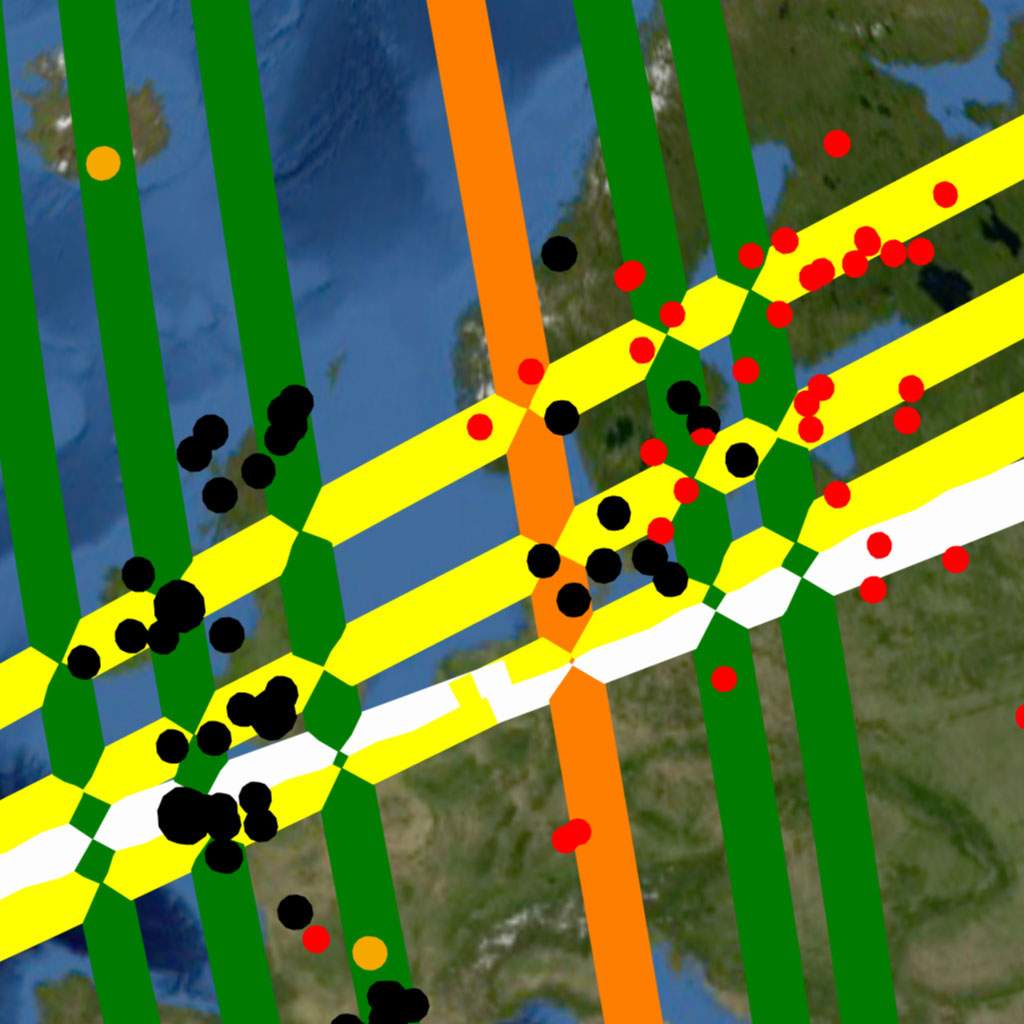



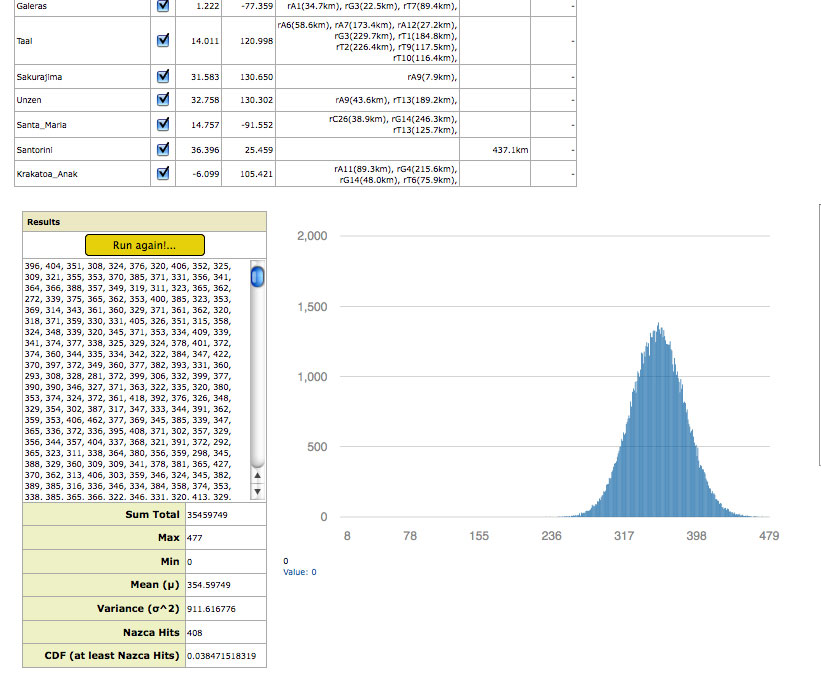

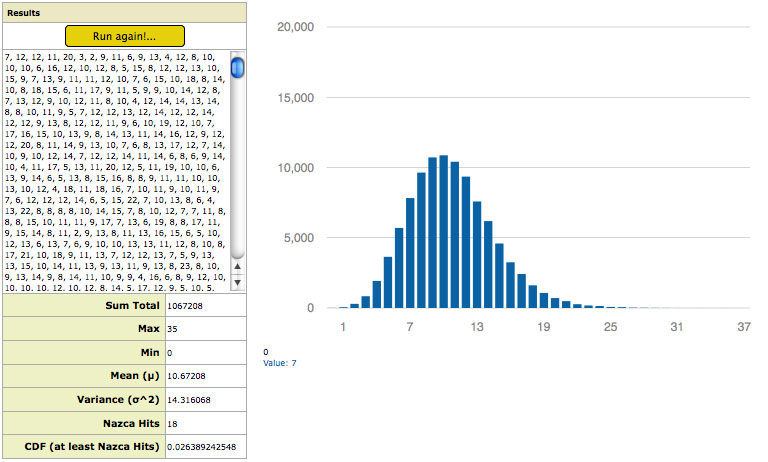
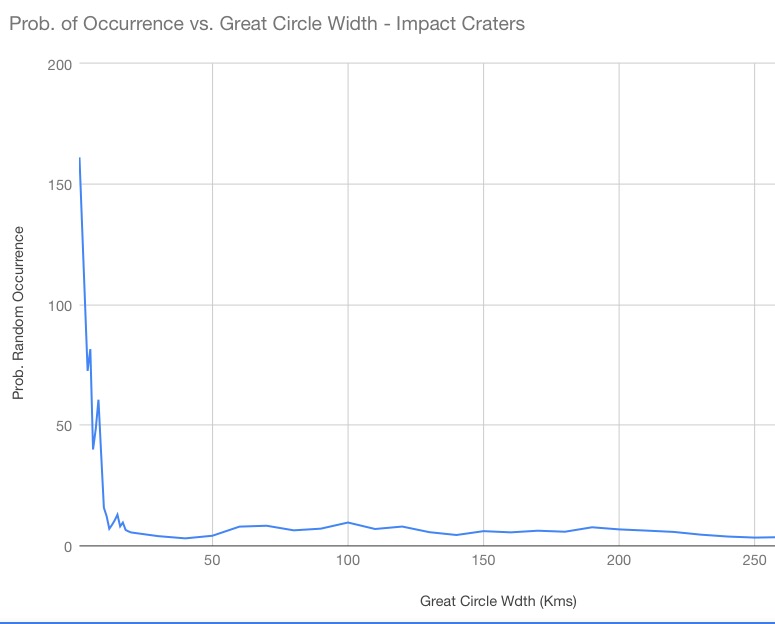

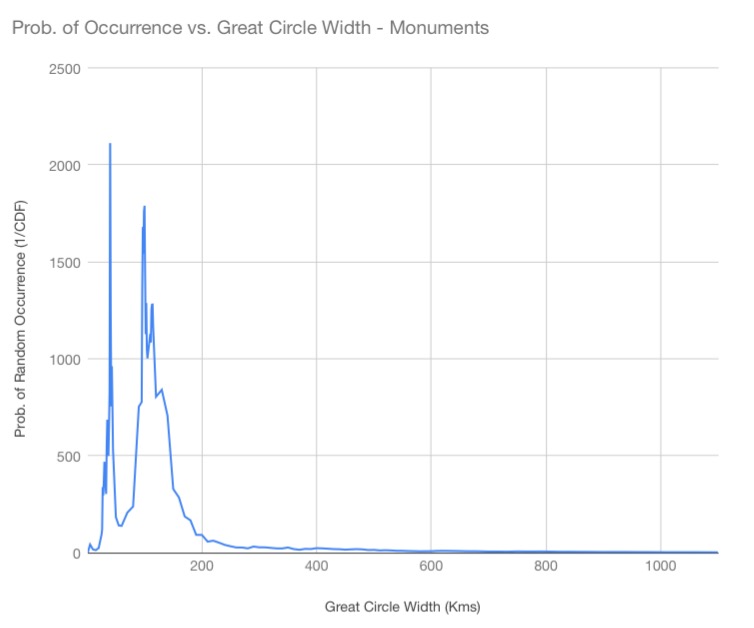

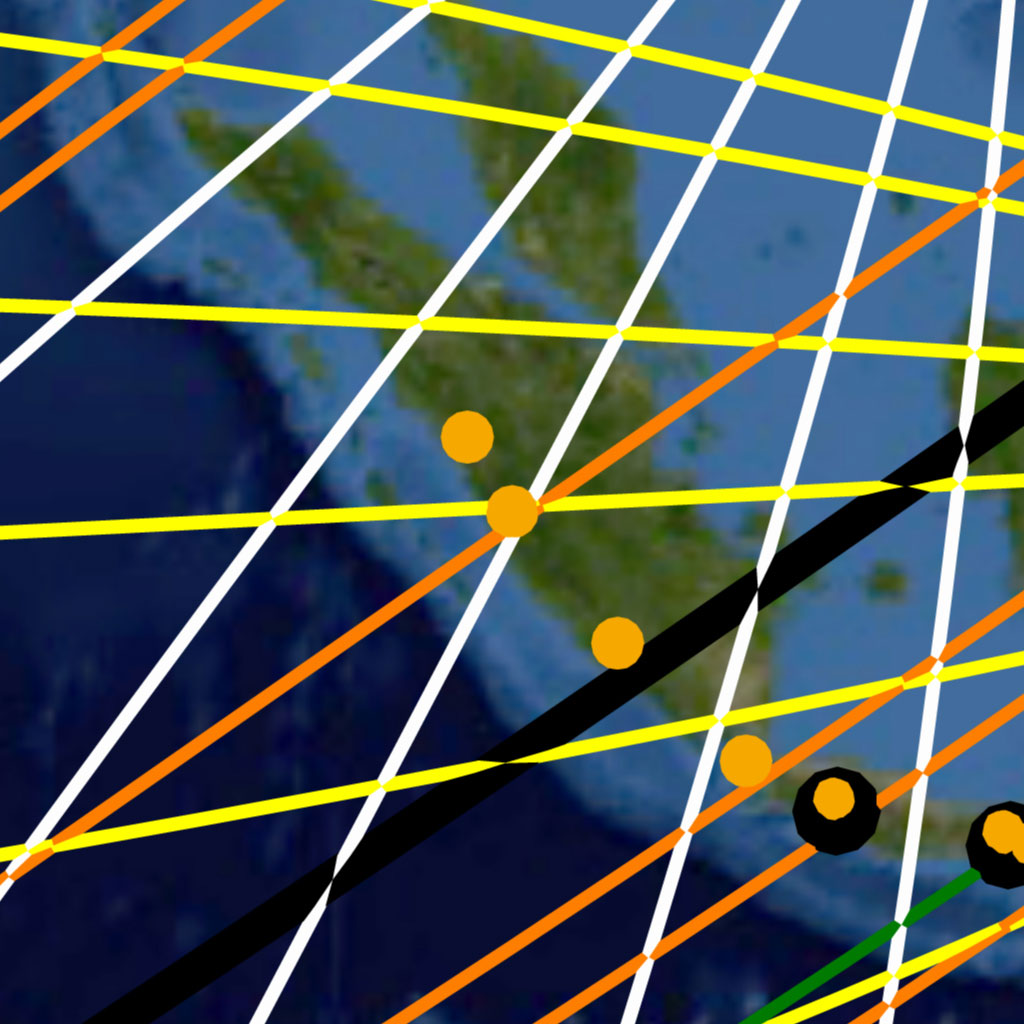
I was impressed. There are ruins in Colombia you never mention, they are older much older than the Incas ruins SAN Agustin ColombiA and Cuevas de tierra adentro and there are much much more in the territory, ciudad perdida, cerró el torrá
Hi Lumaina, thanks for reading and for your comment. The ancient sites were chosen based on being generally recognised and accepted as ancient. That’s not to say that there aren’t many more. There is sort of a limit to how many can be included before the test becomes less meaningful – with thousands of sites covering the land, any random line would naturally intersect many locations – so we have to make a decision on what to include. However, we designed the experiment to be repeatable with any list of sites and we’re working on a user-friendly version that we can add many more sites to. We’ll provide a way for anyone who’s interested to run the experiment themselves, with any additional sites that they’d like to include. We’d be very happy to include the sites you suggest.
Recieve my Congratulations from Chile. I will enjoy analizing this work for a good understanding because it looks really consistent. Thanks to all of you for sharing this results with us. There are a lot of people searching and foundig a lot of material coming from the past in other matters too. Well doing!! -Elizabeth D’Jaures
I think this is an EXCELLENT insight into the Nazca lines – however I might suggest seriously that you take a look at the recent Flat Earth evidence (NOT the flat earth society) – especially the fact that the curvature cannot be found, and also that ancient cultures also understood that the earth was flat (meaning not a globe) this would actually bring more insight, and make absolute sense. Also why they were able to create such straight lines. I suggest the youtube channel Globebusters as a good place to start. I know this is a HOT TABOO subject for so many people, but, the more you look into it, the more you’ll see just how much evidence there is.
Monumental e Fantástico trabalho de descobertas e conexões das origens da Humanidade, não há palavres para elogiar este trabalho e agradecer tamanho esforço de revelações para a humanidade.
Phenomenal! What a great explanation of the genius of our ancestors! And for the first time someone makes sense of the puzzle. Thank you for the enlightening work.
Dear Frank Maglione Nicholson! Great job, congratulations! Years ago, based on my own research, I came to the conclusion that this is a world map. Interested in my hypothesis?
Hi Richárd, answering on behalf of Frank – yes of course, we’d be very interested to hear any hypothesis related to Nazca
Unfortunately, I can’t explain it. Rather, here’s a video. Nasca lines. Line direction.
https://drive.google.com/file/d/16_HWMzqTq90JR3YVvbtFeMrBcn4cYr79/view?usp=drivesdk
Very impressive work!
I would like to follow up on it.
I first learned about the Nazca drawing around around 1970 but only now realised the importance of the discovery.
just an add .. could this map be how and where to place eng directors .. ie obalisk henges ect…. to power the vanhealen belt thing to protec the planet .. just athought
The Nazca lines are messages to the aliens living in the far stars, thanking them for the seed of knowledge they presented to mankind by showing them examples of some of the living creatures and knowledge that humans have.
is your Google Earth overlay sharable? I have a robust set of maps already, and I would love to overlay yours and look for new hypotheses
Could I ask others here to compare what is being presented here to a recent TEDx talk given by Roger G. Gilbertson about a curious earth orbit path which appears to perfectly correlate with this work’s Great Circle R-A?
https://www.youtube.com/watch?v=_HytJn6uaRk&t=
This was excellent. Thank you for the link.
You’re wrong. They are The Orion Groups territory markings to ward off other ETs as to who’s planet this really is or was, Orion’s. They are a 3D star map of their territory. TheOrionLines.com
Surly the radial centres shouldn’t be random in the simulations as they are where they are!
I would ne interested to see results where the RC are fixed but the lines are random, great work
Hi Steve, we did consider this and may have even run some tests with that configuration. In the end we decided that random RCs would be a more genuine test. We’re working on a user-friendly version of the experiment that will be publicly available very soon. We can add an option to use fixed RCs, as you suggest. I’ll keep you posted!
Please. share the google earth source files for this. I have a massive collection of geology work in Google Earth, all towards this particular topic, so I’d love to overlap our research and see what emerges.
It looks like this is part of the programming for Earth in this reality, which in turn is just one of the various other programs that are also running running on this planet and this Universe. Too much to go into here, but that’s the way I see it. This pre-dates humanity.
Frank,
Great work. I remember when your early drafts were much longer and much harder to understand, and Sharif and I were mainly just encouraging you to stay with it. You have clarified it beautifully. Well done.
I am Anishinabe and i live at the foot of ”The Sleeping Giant’ on Fort William First nation in Thunder Bay Ontario Canada. On shore, at the foot of The Sleeping Giant, is an ancient Volcano (Mt. McKay)long dormant.
The Sleeping Giant is part of ‘The Prophecy’; Note, it has no Gender. In fact, if a person stands on the south side of the Bay, the Giant has Female physical attributes (breasts, smaller head). In the middle of the Bay facing East, It takes on masculine features (bigger head, and flat chest). At the North end of the Bay, the female attributes return.
The prophecy speaks of a time when men will be ‘forced’ to bring their feminine energies into a greater balance; women, vice versa. The Sleeping Giant functions as a calendar, a teaching tool and reminder of an old truth (that all human beings are women at conception, gender is chosen later). In fact, The Sleeping Giant is directly online with the Global Grid (see article @ Graham Hancock website, for confirmation RE: Nazca Lines – Google Image 12). We have something called the Three Fire Council; those elders over see the teachings contained in the ‘three fire prophecy’. The teachings contained there-in speak of a time called ‘the world turning over”. From where those elders sit, we are in those times today.
I wish i could share more, and have been given permission to do that by the elders because i am a ‘knowledge keeper in my community – but the requirement for here is to keep it short.
During the time of ‘the world turning over’, our prophecies tell us to share our teachings – this is my attempt to do that. Please be well. Miniiwaniigoshii Benashii (Happy Bird); AKA Robert.
Amazing work this, and thanks Robert for sharing!
Ruapehu in NZ could also represent the Taupo (region) eruptions. https://en.m.wikipedia.org/wiki/Taupo_Volcano
Increadible work! I was doing this over the last couple years on my work computers and also came to the conclusion that the Nazca Lines were a map. I didn’t go into such depth, so this is wonderful to see.
A co-worker of mine pointed out there’s an ancient line that’s been long known in Osoyoos, British Columbia, immediately northwest of the Nk’Mip Winery, within Indigenous lands. Out of curiosity I extended this line as a Great Circle, and doing so led me directly onto a Nazca Line. I haven’t investigated the Osoyoos Line further to see if there are more lines in the region, but I do know there are petroglyphs on lakeside cliffs in the area. Maybe you could check it out.
I was curious as well about what it would look like if these lines were extended outward from the Earth, if there were alignments with stars and constellations.
Its good that they provided a statistical test of their hypothesis. It shows their hypothesis is probably wrong.
The confidence levels they quote for accepting a hypothesis are WAY TOO HIGH. They quote levels of around 5%, or 1%. These are equivalent to around 2 sigma or 3 sigma respectively. Actually, in particle physics, confidence levels of around 0.0001%, or 5 sigma, or less than 1 in 2 million are used. Probabilities of 5% and even 1% occur all the time – they are not scientifically interesting. Even their combined result, that looks at monuments, impact carters etc, only has a confidence level of 1 in 40,000. This is still WAY TOO HIGH to be scientifically interesting.
In any case, their test is flawed because they have complete freedom to choose the variables. Their method for selecting ‘centres’ from which the great circles radiate is completely arbitrary. It allows them complete freedom to choose these centres as they like, thus biasing the test.
So my opinion is that this is nonsense, and their statistical test actually shows this to be the case.
Just a quick proof-reading comment if I may! You list ‘Silsbury Hill’, but I think you mean ‘Silbury’, near Avebury. Maybe it’s got confused with the nearby city of Salisbury!