It remains one of the most scrutinised structures in the world and still its secrets remain largely elusive to us. The Great Pyramid at Giza stands 481 feet tall with each of its four base lengths measuring almost exactly 756 feet. But why did the ancient designers of this structure decide upon these particular dimensions? What rationale might they have used – or were these dimensions merely the arbitrary product of a whimsical desire on the part of the Pharaoh Khufu, in whose the name the Great Pyramid of Giza was apparently built?
It would seem, however, that whimsical or arbitrary dimensions were far from the minds of the designers of the Great Pyramid. As we further explore this question, we will discover that the dimensions of the Great Pyramid may well have been formed on a scientific basis. We will find also that the ancient Egyptian measure – the Royal Cubit – may also have originally been derived from this hitherto unknown ancient science.
Before the construction of a pyramid can even begin there would naturally be a plan, or indeed a number of plans, giving the dimensions, angles and so forth to a particular scale. The practical need for such would have been every bit as essential in ancient times as it is to us here in the 21st century. Though no plans of Khufu's Pyramid have ever been found, it is quite inconceivable to consider that such a massive undertaking could have been achieved without the use of plans of some kind. It is further unlikely that the implementation – i.e. the scaling up – of any such architectural plan(s) could have been achieved without having first developed a standard unit of linear measure.
The standard unit of measure used by the ancient Egyptians was the Royal Cubit or Mahe which would be equivalent to 20.61 inches. This measure was subdivided into 7 palms of 4 digits each, giving a Royal Cubit unit measure of 28 equal parts. Conventional wisdom informs us that the ancient Egyptians defined the length of the Royal Cubit by averaging the length of a man's forearm – from his elbow to the tip of his middle finger. It is unsurprising, therefore, that the ancient Egyptian hieroglyph for their Royal Cubit measure is symbolised by the forearm. But should the fact that the Royal Cubit is symbolised by the forearm automatically imply that the forearm was the original means by which the Royal Cubit was derived? Or could it be equally possible that the forearm hieroglyph is actually (unwittingly) symbolising a scientifically based unit of measure whereby, as a result of the male forearm being a very close approximation to the underlying scientifically-based length, the forearm symbol was then used to depict the measure?
So, what is this scientifically grounded method of deriving the ancient Egyptian's Royal Cubit? And what evidence is there that might support the hypothesis that the Royal Cubit length was originally based in science? To begin to answer these questions we must first attempt to understand the process of creating a measuring system.
A CONSISTENT MEASURE
Virtually anything – a leaf, a rock, a toe, etc – could be used as the basis of a measuring system provided everyone within a particular community or society agrees on the particular object being used. If, for example, a seashell was used as the base unit of linear measure, then rulers or "rods" can be made to the exact length of this seashell which craftsmen can then use to design and build things to the "seashell standard". If, however, one of these seashell rods is measured from another rod which is, in turn, measured to create another rod then, over time, the unit of measure will inexorably "drift" in accuracy from the original seashell length. To create a perfect rod length each and every time then it would naturally be best to create the rod from the original source, the seashell, each and every time a rod was required. In this way the measure is much less likely to drift in its accuracy, producing rod after rod of equal and consistent length.
If, however, the original source measure (the seashell) became lost or was otherwise inaccessible for some reason then a replacement seashell would not give the exact same measure as the previous seashell measure – the original unit of measure. In effect a whole new measuring system – and everything this implies – would have to be created. And then if this seashell was somehow also lost…..
The master builders of ancient times would have been every bit as aware of this potential problem as we are today. They would have realised that a better solution to their measure – to prevent the scenario outlined above from ever happening – would be to define a unit of measure that was itself based on some entity or property that would consistently give the same length. And even if the original measure became lost or was destroyed, the unit could simply and easily be re-created from scratch.
But what?
In 1790 Thomas Jefferson – some 11 years before he became President of the United States – was charged with the task of defining a new unit of weights and measures for the fledgling new country. In consideration of the problem of devising a standard unit of measure, Jefferson wrote:
"There exists not in nature, as far as has been hitherto observed, a single subject or species of subject, accessible to man, which presents one constant and uniform dimension."
In their ground-breaking book Civilisation One (Watkins, 2004), authors Christopher Knight and Alan Butler, through their analysis of Scottish Engineer, Alexander Thom's Megalithic Yard, came to the very same conclusion as Jefferson. And indeed, as I grappled with the question of finding a possible scientific source to the ancient Egyptian Royal Cubit, I found myself also arriving at this conclusion. The natural world simply does not produce anything that is easily accessible and consistently of the same length that could be used as the underlying basis for a unit of measure. Even if we take an average length of a man's forearm, will this average be the same in ancient times as it is today when much of the western world has been "super-sized" with all manner of junk food, making us larger than our ancestors? Probably not.
It may well be that nature is unable to produce two items that are consistently exactly the same length but there are, however, other aspects to our planet that are indeed considered generally consistent and easily accessible – its rotation and its gravity! But is it possible to create a linear unit of measure from these two properties of the Earth?
Indeed it is. Furthermore, in defining such a unit of measure from these two properties (rotation and gravity), we will be producing a unit of measure that is equivalent to the ancient Egyptian Royal Cubit of 20.61 inches and – in so doing – perhaps we may also be rediscovering the very method by which the Royal Cubit was originally devised.
TIME AND GRAVITY
When a leaf flutters to the ground in an autumn breeze, it does so as a result of gravitational forces. Newton was the first to recognise this fundamental natural force; a force that affects every part of our existence here on Earth. Gravitational force is pretty much the same all over the planet with very negligible variations. If, for example, you were to drop a ball or some other heavy object from a tower that is, for example, 16 feet high, it will take that object almost exactly 1 second to hit the ground. Provided the object is always dropped from the same height (16 feet), then it will always take 1 second for the object to reach the ground. And, as stated, this effect is more or less consistent all over the world with very slight but negligible latitudinal variation.
We can say then that 1 second of Earth time is equal to 16 "gravity feet" (i.e. the distance an object will fall in 1 second of time). One full Earth day would then be equal to 261.81 miles i.e. 86,400 (seconds per day) x 16 gravity feet = 1,382,400 feet. It doesn't matter if we drop a ton or a kilogramme – both will fall at the same rate, reaching the ground at the same time. And what's more – this will never change. By allowing an object to fall for precisely 1 second of time, we will require to construct a "drop tower" that is 16 feet high. Thus we have a unit of measure (16 feet) that is defined by time and gravity; a unit of measure that can be consistently reproduced virtually anywhere on Earth and in any age.
Of course, calibrating a drop tower to produce a drop height of exactly 1 second duration would be problematic, if not impossible. One second of time is simply too quick for humans – especially in ancient times – to have measured. If the duration was longer – say 5 or 10 seconds – this would make calibrating the drop height much easier. However, this does not simply mean constructing a drop tower that is 5 x 16 feet. Although gravity is constant, it also causes falling objects to constantly accelerate! This means that the higher the drop becomes the quicker a falling object will be allowed to travel to reach the ground because the falling object (excluding external factors such as wind resistance) is continually building up speed as it falls (gravitational acceleration). The effect of this means that for an object to fall for a duration of 5 seconds would require a drop tower of over 400 feet! Clearly this would be quite impractical – there has to be a simpler method of using time and gravity to define a linear unit of measure.
THE PENDULUM
Gravitational force acting upon a simple pendulum can produce a very similar effect but without the need to build a drop tower of over 400 feet. To achieve a 2 second pendulum swing (i.e. 1 second outward swing and 1 second return swing) requires the pendulum cord length to be a fraction over 3.25 feet (39 inches) in length – much more practical and manageable. By calibrating the swing of the pendulum by the use of a 30 second hourglass or water clock until the pendulum produces exactly 30 swings to the 30 second timer means that the ancients could not have failed to produce a pendulum cord length of a fraction over 39 inches. Gravity dictates it! A longer cord length would produce too few swings within the 30 second timer whereas a shorter cord length would produce too many swings within the same period.
And so we have defined the "Gravity Cubit". And once again this unit of measure will be almost identical all over the Earth with a negligible fluctuation in the gravitational force resulting in the tiniest fractional difference in the pendulum cord length – so small in fact as to be considered negligible. It is also worth noting here that the Gravity Cubit is almost identical in length to the modern metre which measures 39.37 inches!
The height of the Great Pyramid is 5,772 inches. This, in turn, is equal to 148 Gravity Cubits (5772 ÷ 39). But why 148 Gravity Cubits? Why not a nice rounded number like 150 Gravity Cubits? What is so significant or special about the number 148?
The answer to this problem presented itself to me in one of ancient Egypt's most enigmatic and puzzling hieroglyphs – the Akhet (Figure 1).

Figure 1 – 'Ahket Khufu' Hieroglyph
Could it be that the height of the Great Pyramid of Khufu – 148 Gravity Cubits -was determined by the setting sun i.e. the duration it takes the sun to set at Giza as depicted in the Ahket hieroglyph? If this was to remain possible then the setting sun at Giza should take 148 seconds (148 x 39" = 5,772").
Quite incredibly, on the autumn equinox at Giza it takes the sun precisely 147.757 seconds to set from when the lower rim of the solar disc of the sun first touches the horizon until the upper rim of the solar disc fully sets below it. Naturally it would make sense for the ancient designers to round up this sunset duration to 148 seconds since it is inconceivable that they would have been able to measure precisely a fraction of one second; a fraction of one swing of a pendulum.
Thus the height of the Great Pyramid of Khufu can be defined by the Gravity Cubit (39 inches) multiplied by the duration of the sunset at Giza at the autumn equinox (148 seconds). And the base of the Great Pyramid being in a ratio of 1.571 to the pyramid's height is equivalent to 232.51 Gravity Cubits (9,067 inches). But how do we then find the ancient Egyptian Royal Cubit from the Gravity Cubit?
By simply adding the height and width of the Great Pyramid together we find the value of 14,839 inches. This is an interesting figure in its own right simply by virtue of the fact that it demonstrates the key values of 148 and 39! We have found through the use of time (148 seconds) that we can define the height of the Great Pyramid. If we simply extend this idea of time and use the number of minutes in half of 1 solar day (720 minutes) we find the ancient Egyptian Royal Cubit 14839 ÷ 720 = 20.61 inches. The Royal Cubit then may well have been based upon the dimensions of the Great Pyramid divided by the number of minutes in half of one solar day. And given that the average length of a man's forearm also approximates this length, this glyph may have been used to symbolise the measure.
There are other curious aspects linking the Great Pyramid's dimensions with time. Take, for example, its slope angle of 51.84º. The ancient Egyptians used a 360 day calendar and added an extra 5 epagomenal days at the end of each year to give a 365 day calendar. Excluding the epagomenal days, we find in 1 Egyptian year there are 31,104,000 seconds. In 1 leap year of 366 days there are 31,622,400 seconds. This represents a difference of 518,400 seconds and in this we are reminded of the slope angle of the Great Pyramid.
If this wasn't curious enough, we then find that the 365 day year x 16 (feet) = 5,840 x 720 minutes (half of 1 solar day) = 4,204,800 inches = 350,400 feet. This figure just happens to be almost exactly the sum of the Great Pyramid's perimeter of 3,024 feet + its height of 481 feet = 3,505 feet (x 100) = 350,500 feet.
Furthermore, if we then take 10,000,000 times the distance between G1 to G3 pyramid centres, then the time it would take an object to fall this length is 43,725 seconds which gives us 12 hours, 8 minutes and 45 seconds.
It so happens that this time period is the time it takes the sun to traverse the sky from sunrise to sunset at the autumn or vernal equinoxes at Giza!
The Great Pyramid – a monumental expression of time and space.
Before finally leaving the Gravity Cubit it is also worth noting that the height of the Great Pyramid (5,772 inches) when divided by Phi (1.618034) reduces this height to almost exactly 1 inch after 18 divisional iterations, thus:
| 5772.00 |
| 3567.29 |
| 2204.71 |
| 1362.58 |
| 842.12 |
| 520.46 |
| 321.66 |
| 198.80 |
| 122.86 |
| 75.93 |
| 46.93 |
| 29.00 |
| 17.93 |
| 11.08 |
| 6.85 |
| 4.23 |
| 2.62 |
| 1.62 |
| 1.00 |
Thus the height of the Great Pyramid divided by 18 iterations of Phi may also have been the original source of the humble inch. It may also help explain this quite remarkable expression of the Phi spiral in the Great Pyramid discovered by the author, Gary Osborn:
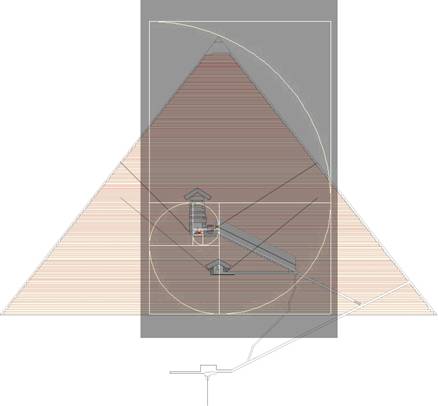
Figure 3 – The Great Pyramid Phi Spiral
(Diagram courtesy of Gary Osborn)
HEAVENLY DESIGNS
Of course, critics of the "Gravity Cubit" hypothesis will undoubtedly point to the fact that the ancient Egyptian Royal Cubit was in use hundreds of years before the Great Pyramid at Giza was built therefore it would have been impossible for its dimensions to have influenced the unit of measure in the manner proposed. The simple fact is, however, there is no need to physically build the Great Pyramid in order to have determined what its eventual dimensions would be. A scaled plan for the Great Pyramid (along with the other Giza pyramids) could have been devised long before a single block of any pyramid was ever set in place. The plan's scale would naturally have been based upon the "Gravity Cubit" and incorporated into any plan. In this regard it is interesting that the Great Pyramid's height consists of 280 Royal Cubits with the cubit measure itself divided into 28 equal parts thus perhaps demonstrating a 1:10 scale.
But what do the ancient Egyptians say of such plans? Interestingly, etched into the stonework in the colonnade of the Temple of Horus at Edfu there is to be found the following curious inscription in ancient Egyptian hieroglyphs:
"They [the temples] were built according to an architectural plan which was supposed to have been revealed in a codex that fell from the heavens at Saqqara in the days of Imhotep."
What this inscription seems to imply is that the structure that the great vizier, Imhotep, built for the 3rd Dynasty Pharaoh Djoser at Saqqara – the world's first Step Pyramid – was actually constructed from a plan that had apparently come, not from the ancient Egyptians (AEs) of the 3rd Dynasty (or, indeed, from any AE dynasty), but from somewhere else; from some earlier time. It further implies that every "temple" from Imhotep's time to those constructed by much later Egyptian dynasties was based upon this ancient "codex" from "heaven". It would seem then that, although Imhotep probably oversaw and engineered the actual construction of Djoser's Step Pyramid at Saqqara, he apparently was not its architect – the plan was "revealed" to Imhotep. Who the original architects of this "heavenly codex" were will likely remain a mystery.
Assuming that such architectural plans were indeed passed down through generations of the ancient Egyptian civilisation in some form, it seems somewhat improbable that the implementation of any such architectural plans by the AEs would have occurred immediately. Further assuming that the plan or "codex" was a three-dimensional model of the Giza Pyramids (perhaps crafted in durable granite), then it is logical to consider that the builders would first have to familiarise themselves with the craft of constructing the pyramid form before even attempting to make manifest their "sacred plan". And from the evidence we see in Egypt today and from the ancient record, we do indeed find a natural evolution of the pyramid form having taken place from Djoser's Step Pyramid at Saqqara to the smooth-sided Red Pyramid of the Pharaoh Snefru at Dahshur.
Along the learning-curve to achieving their goal of constructing smooth-sided pyramid structures, it is unsurprising that many mistakes were made. Pyramids were built on ground that was – all too late – found to be too unstable. Pyramid slopes were constructed at too steep an angle, causing the structure to collapse under its own weight. Eventually, however, having learned from their past mistakes, the builders eventually managed to construct the world's first stable, smooth-sided, "true pyramid" – the Red Pyramid at Dahshur.
And so, having finally secured the craft of constructing stable, true pyramids, the time to fully implement their ancient "codex" had arrived – the construction of the Pyramids of Giza, finally implemented by the 4th Dynasty Egyptians in quite stunning fashion.
Acknowledgments:
In forming the Gravity Cubit hypothesis, the author sincerely wishes to thank the following individuals for their valued assistance and insights:
Don Barone
Stephen W. Dail
Gary Osborn
Spiros Boutsikos
Geoff Simmons
Derek Skhane
Mike Nordberg
Tommi Huhtamaki
Dale Robert Lerch
James Kellams





